题目内容
17.将一个圆形转盘的盘面按1~2~3~4分成四个部分,依次涂上红,黄,蓝,绿四种颜色,自由转动转盘,停止后指针落在绿色区域的概率为$\frac{2}{5}$.分析 首先确定在图中绿色区域的面积在整个面积中占的比例,根据这个比例即可求出指针指向绿色区域的概率.
解答 解:∵圆被等分成10份,其中绿色部分占4份,
∴落在绿色区域的概率=$\frac{4}{10}$=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题考查几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率;

练习册系列答案
相关题目
12.若m为整数,则能使$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$也为整数的m有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.若a、b是关于x的一元二次方程x2-6x+n+1=0的两根,且等腰三角形三边长分别为a、b、4,则n的值为( )
| A. | 8 | B. | 7 | C. | 8或7 | D. | 9或8 |
9.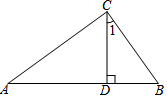 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠1的值为( )
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠1的值为( )
 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠1的值为( )
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BC=3,AC=4,则sin∠1的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
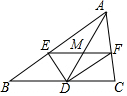 如图,在△ABC中,D是BC上的一点,DE平分∠ADB,DF平分∠ADC,且EF∥BC,若EF交AD于M,EF=18,则DM=9.
如图,在△ABC中,D是BC上的一点,DE平分∠ADB,DF平分∠ADC,且EF∥BC,若EF交AD于M,EF=18,则DM=9.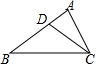 如图,点D是△ABC的AB边上一点,且AB=6,BD=4,AC=2$\sqrt{3}$.
如图,点D是△ABC的AB边上一点,且AB=6,BD=4,AC=2$\sqrt{3}$.