题目内容
12.若m为整数,则能使$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$也为整数的m有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 首先将原式分子与分母分解因式,进而化简,再将符合题意的m值代入即可.
解答 解:∵$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$=$\frac{(m-1)^{2}}{(m+1)(m-1)}$=$\frac{m-1}{m+1}$,
∴能使$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$也为整数的m有:m=1或m=-2或m=-3,
故选:C.
点评 此题主要考查了约分以及代数式求值,正确因式分解是解题关键.

练习册系列答案
相关题目
4.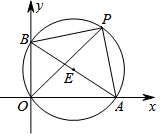 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,2),P是△AOB外接圆上一点,且∠AOP=45°,则P点到x轴的距离为( )| A. | $\sqrt{6}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{6}+\sqrt{2}$ | D. | $1+\sqrt{3}$ |
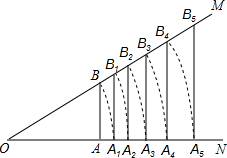 如图,已知∠MON=30°,AB⊥ON,垂足为点A,点B在射线OM上,AB=1cm,在射线ON上截取OA1=OB,过A1作A1B1∥AB,A1B1交射线OM于点B1,再在射线ON上截取OA2=OB1,过点A2作A2B2∥AB,A2B2交射线OM于点B2;…依次进行下去,则A1B1线段的长度为$\frac{2\sqrt{3}}{3}$,A6B6线段的长度为${2}^{6}(\frac{\sqrt{3}}{3})^{6}$.
如图,已知∠MON=30°,AB⊥ON,垂足为点A,点B在射线OM上,AB=1cm,在射线ON上截取OA1=OB,过A1作A1B1∥AB,A1B1交射线OM于点B1,再在射线ON上截取OA2=OB1,过点A2作A2B2∥AB,A2B2交射线OM于点B2;…依次进行下去,则A1B1线段的长度为$\frac{2\sqrt{3}}{3}$,A6B6线段的长度为${2}^{6}(\frac{\sqrt{3}}{3})^{6}$.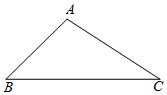 如图,在△ABC中,∠B=45°,∠C=30°,AB=4$\sqrt{2}$,求AC和BC的长.
如图,在△ABC中,∠B=45°,∠C=30°,AB=4$\sqrt{2}$,求AC和BC的长.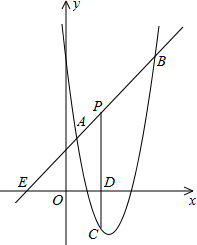 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A($\frac{1}{2}$,$\frac{5}{2}$)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.