题目内容
7．
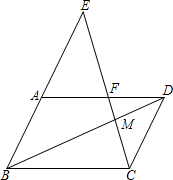如图，在四边形ABCD中，AB∥CD，点F在边AD上，BA的延长线交CF的延长线于点E，EC交BD于点M，且CM2=EM•FM．求证：AD∥BC．
分析 首先利用AB∥CD，得出△BEM∽△CDM，进而利用相似三角形的性质得出比例式之间关系，求出即可．
解答 证明：∵AB∥CD，
∴△BEM∽△CDM，
∴$\frac{BM}{DM}$=$\frac{EM}{CM}$，
∵CM2=EM•FM．
∴$\frac{EM}{CM}$=$\frac{CM}{FM}$，
∴$\frac{BM}{DM}$=$\frac{CM}{FM}$，
∴AD∥BC．
点评 此题主要考查了相似三角形的判定与性质，利用平行得出△BEM∽△CDM是解题关键．
练习册系列答案
相关题目
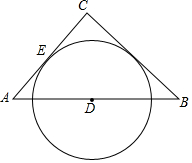如图，△ABC中，CA=CB，D为AB的中点，以D为圆心的圆与AC相切于点E，求证：BC与⊙O相切．
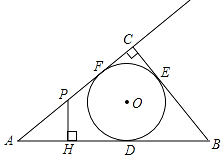如图，Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F，且∠ACB=90°，AB=5，BC=3，点P在射线AC上运动，过点P作PH⊥AB，垂足为H．
12．下列说法中正确的是（ ）
| A． | 近似数0.66有两个有效数字 | B． | 近似数5.01×103精确到百分位 | ||
| C． | 近似数2.10精确到十分位 | D． | 近似数5.8万精确到万位 |
如图，⊙O的半径为$\sqrt{2}$，圆周角∠BAC=135°，求BC的长．
小敏在作⊙O的内接正五边形时．先做了如下几个步骤：