Question

14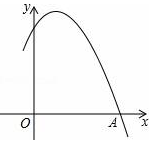．如图是二次函数y=ax²+bx+c图象的一部分，其图象的对称轴是直线x=1，且过点A（3，0），则下列结论正确的是（　　）

• A． ac＞0
• B． 4a+2b+c＜0
• C． a-b+c＞0
• D． b²＞4ac

Answer 1

分析 根据抛物线与x轴有两个交点有b²-4ac＞0可对A进行判断；由抛物线开口向下得a＜0，由抛物线与y轴的交点在x轴上方得c＞0，则可对B进行判断；根据抛物线的对称性得到抛物线与x轴的另一个交点为（-1，0），所以a-b+c=0，则可对C选项进行判断；由于x=2时，函数值大于0，则有4a+2b+c＞0，于是可对D选项进行判断．

解答 解：∵抛物线开口向下，
∴a＜0，
∵抛物线与y轴的交点在x轴上方，
∴c＞0，
∴ac＜0，所以A选项错误；
∵当x=2时，y＞0，
∴4a+2b+c＞0，所以B选项错误；
∵抛物线过点A（3，0），二次函数图象的对称轴是x=1，
∴抛物线与x轴的另一个交点为（-1，0），
∴a-b+c=0，所以C选项错误；
∵抛物线与x轴有两个交点，
∴b²-4ac＞0，即b²＞4ac，
所以D选项正确．
故选D．

点评 本题考查了二次函数的图象与系数的关系：二次函数y=ax²+bx+c（a≠0）的图象为抛物线，当a＞0，抛物线开口向上；对称轴为直线x=-$\frac{b}{2a}$；抛物线与y轴的交点坐标为（0，c）；当b²-4ac＞0，抛物线与x轴有两个交点；当b²-4ac=0，抛物线与x轴有一个交点；当b²-4ac＜0，抛物线与x轴没有交点．