题目内容
16．已知抛物线的顶点在原点，对称轴为y轴，且经过点（2，-4），则抛物线的解析式为y=-x2．分析 根据图象顶点为原点得到抛物线的c值为0，再由对称轴为y轴，得到b=0，设出适当的表达式，把（2，-4）代入设出的表达式中，求出a的值，即可确定出抛物线的表达式．
解答 解：∵抛物线的顶点在原点，对称轴是y轴，
∴设此抛物线的表达式是y=ax2，
把（2，-4）代入y=ax2中得：-4=4a，解得：a=-1，
则此抛物线的表达式是y=-x2．
故答案为：y=-x2
点评 此题考查了待定系数法求二次函数的解析式，解答本题的关键是设出适当的解析式．
练习册系列答案
相关题目
6．如果a是负数，那么-a2，2a，a+|a|，$\frac{a}{|a|}$这四个数中，是负数的个数为（ ）
| A． | 1个 | B． | 2个? | C． | 3个 | D． | 4个 |
4．将x2-3ax-6ab-4b2因式分解，分组方法正确的是（ ）
| A． | （x2-3ax）-（6ab-4b2） | B． | （x2-6ab）-（3ax-4b2） | C． | （x2-4b2）+（-3ax-6ab） | D． | （x2-3ax）-（6ab-4b2） |
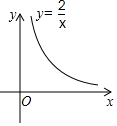已知点A（1，y1），B（2，y2）是如图所示的反比例函数y=$\frac{2}{x}$图象上两点，则y1＞y2（填“＞”，“＜”或“=”）．
有理数a、b、c在数轴上的位置如图所示，那么|a-b|-|1-b|+|c-1|=2-a-c．