题目内容
19. (1)商店有A、B、C、D四种饮料,每种饮料数量充足,某同学去该店购买饮量,每种饮料被选中的可能性相同.
(1)商店有A、B、C、D四种饮料,每种饮料数量充足,某同学去该店购买饮量,每种饮料被选中的可能性相同.①若他去买一瓶饮料,求他买到A饮料的槪率;
②若他两次去买饮料,每次买一瓶,且两次所买饮枓不同,求他恰好买到A和B饮料的概率.
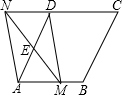
(2)如图,菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是 AB边上一动点(不与点A重合),连接ME并延长交CD的延长线于点N,连接MD、AN.
①求证:四边形AMDN是平行四边形;
②当AM为何值时,四边形AMDN是矩形?
分析 (1)①直接利用概率公式求解;
②先画树状图展示所有12种等可能的结果数,再找出买到A和B饮料的结果数,然后根据概率公式求解;
(2)①先根据菱形的性质得AB∥CD,则利用平行线的性质得∠DNM=∠AMN,于是可利用“AAS”判定△AME≌△DNE,得到AM=DN,加上AM∥DN,则可根据平行四边形的判定方法得到四边形AMDN是平行四边形;
②根据矩形的判定方法,当MN=AD时,即AE=EM时,四边形AMDN是矩形,利用四边形ABCD为菱形可得AD=AB=2,则AE=2,接着判断△AEM为等边三角形,得到AM=2,即当AM为2时,四边形AMDN是矩形.
解答 (1)解:①他买到A饮料的槪率=$\frac{1}{4}$;
②画树状图为:
共有12种等可能的结果数,其中买到A和B饮料的结果数为2,
所以他恰好买到A和B饮料的概率=$\frac{2}{12}$=$\frac{1}{6}$;
(2)①证明:∵四边形ABCD为菱形,
∴AB∥CD,
∴∠DNM=∠AMN,
∵点E是AD边的中点,
∴AE=DE,
在△AME和△DNE中,
$\left\{\begin{array}{l}{∠AME=∠DNE}\\{∠AEM=∠DEN}\\{AE=DE}\end{array}\right.$,
∴△AME≌△DNE,
∴AM=DN,
而AM∥DN,
∴四边形AMDN是平行四边形;
②解:∵四边形AMDN是平行四边形,
∴当MN=AD时,即AE=EM时,四边形AMDN是矩形,
∵四边形ABCD为菱形,
∴AD=AB=2,
∴AE=2,
而∠DAB=60°,
∴△AEM为等边三角形,
∴AM=2,
即当AM为2时,四边形AMDN是矩形.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了列表法与树状图法、平行四边形和矩形的判定.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案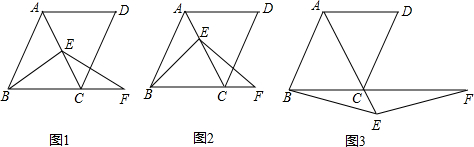
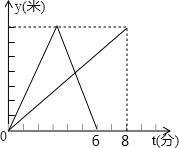 小华和爷爷在一环形跑道上匀速跑步,两人在同一起点顺时针出发,两人离起点较近的环形距离y与时间t之间关系如图所示,出发后小华第一次与爷爷相遇的时间为9.6分.
小华和爷爷在一环形跑道上匀速跑步,两人在同一起点顺时针出发,两人离起点较近的环形距离y与时间t之间关系如图所示,出发后小华第一次与爷爷相遇的时间为9.6分.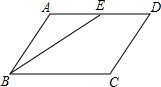 如图,在平行四边形ABCD中,点E为AD的中点,试用无刻度的直尺分别在四边形的内部和外部各画一个与△ABE全等的三角形.
如图,在平行四边形ABCD中,点E为AD的中点,试用无刻度的直尺分别在四边形的内部和外部各画一个与△ABE全等的三角形. 如图,?ABCD中,E为AD的中点,BE,CD的延长线相交于点F,若△DEF的面积为1,则?ABCD的面积等于4.
如图,?ABCD中,E为AD的中点,BE,CD的延长线相交于点F,若△DEF的面积为1,则?ABCD的面积等于4.