题目内容
7.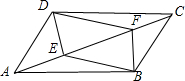 如图,在?ABCD中,E,F是对角线AC上两点
如图,在?ABCD中,E,F是对角线AC上两点(1)若AE=CF,则四边形DEBF是平行四边形吗?请说明理由;
(2)当BE与DF满足什么条件时,四边形DEBF是平行四边形?请说明理由.
分析 (1)由平行四边形的性质得出OA=OC,OB=OD,再由已知条件得出OE=OF,即可得出结论;
(2)由平行四边形的性质得出OB=OD,由平行线的性质得出∠BEF=∠DFE,由AAS证明△BOE≌△DOF,得出对应边相等,即可得出结论.
解答 解:(1)四边形DEBF是平行四边形;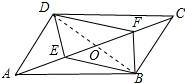 理由如下:连接BD,如图所示:
理由如下:连接BD,如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形.
(2)当BE∥DF时,四边形DEBF是平行四边形;理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,
∵BE∥DF,
∴∠BEF=∠DFE,
在△BOE和△DOF中,
$\left\{\begin{array}{l}{∠BEF=∠DFE}&{\;}\\{∠BOE=∠DOF}&{\;}\\{OB=OD}&{\;}\end{array}\right.$,
∴△BOE≌△DOF(AAS),
∴BE=DF,
又∵BE∥DF,
∴四边形DEBF是平行四边形.
点评 本题考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的性质;熟练掌握平行四边形的判定与性质,证明三角形全等是解决问题(2)的关键.

练习册系列答案
相关题目
15.小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬按16元/时计算,设小明的哥哥这个月工作的时间为t小时,应得报酬为m元,填写下表后回答下列问题:
(1)在上述问题中,哪些是常量?哪些是变量?
(2)能用含t的代数式来表示m的值吗?
| 工作时间t(小时) | 1 | 5 | 10 | 15 | 20 | … |
| 报酬m元 | 16 | 80 | 160 | 240 | 320 |
(2)能用含t的代数式来表示m的值吗?
 如图是“宝真商场”中某洗发水的价格标签,那么这种洗发水的原价是24元.
如图是“宝真商场”中某洗发水的价格标签,那么这种洗发水的原价是24元.
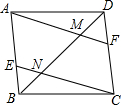 如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.
如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.