Question

19．动手操作：在小学我们利用拼图的方法得到三角形内角和为180°．
如图1，把△ABC分成三部分，然后以顶点C为中心，把三个角拼在一起构成平角，如图所示，从而得到三角形内角和是180°

说明论证：
根据拼图过程，小明给出了不完整的说理过程，请按小明的思路补全说理过程．
已知：如图2，在△ABC，∠A、∠B、∠C是三角形的三个内角；
 说明：∠A+∠B+∠C=180°
 理由：延长BC到点D，过点C作CE∥AB，（补全辅助线作法，并在图2中作出辅助线来）
∴∠A=∠1；∠B=∠2
∵∠ACB+∠1+∠2=180°（平角定义）
∴∠A+∠B+∠C=180°（等量代换）
简单应用：
在△ABC，∠A比∠C大35°、∠B比∠A大5°，求△ABC三个内角度数；
拓展归纳：
（1）如图3，在四边形ABCD中，连接AC，则∠ABC+∠BCD+∠D+∠DAB的度数？（直接写结果）
（2）如图4，在五边形ABCDE中，则∠A+∠B+∠C+∠D+∠E的度数？（直接写结果）
（3）猜想：在n边形ABCDE…R中，则∠A+∠B+…∠E+∠R的度数？（直接写结果）

Answer 1

分析 说明论证：延长BC到点D，过点C作 CE∥AB，由平行线的性质得出∠A=∠1，∠B=∠2，再由平角的定义即可得出结论；
简单应用：根据题意得出∠C=∠A-35°，∠B=∠A+5°，由三角形内角和定理得出∠A+∠A+5°+∠A-35°=180°，解方程求出∠A=70°，即可得出∠B、∠C的度数；
拓展归纳：（1）在△ABC和△ACD中，由三角形内角和定理得出∠BAC+∠B+∠ACB=180°，∠DAC+∠ACD+∠D=180°，即可得出结论；
（2）连接AC、AD，在△ABC、△ACD、△ADE中，由三角形内角和定理得出∠BAC+∠B+∠ACB=180°，∠DAC+∠ACD+∠ADC=180°，∠DAE+∠ADE+∠E=180°，即可得出结论；
（3）由三角形内角和、四边形内角和、五边形内角和得出规律，即可得出结果．

解答 解：说明论证：
已知：如图2，在△ABC，∠A、∠B、∠C是三角形的三个内角；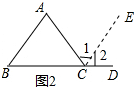
 说明：∠A+∠B+∠ACB=180°
 理由：延长BC到点D，过点C作 CE∥AB，如图2所示：
∴∠A=∠1，∠B=∠2，
∵∠ACB+∠1+∠2=180°（平角定义）
∴∠A+∠B+∠ACB=180°（等量代换）；
故答案为：CE∥AB，∠1，∠2；∠1，∠2；
简单应用：
解：根据题意得：∠C=∠A-35°，∠B=∠A+5°，
∵∠A+∠B+∠ACB=180°，
∴∠A+∠A+5°+∠A-35°=180°，
解得：∠A=70°，
∴∠B=75°，∠C=35°；
拓展归纳：
解：（1）∠ABC+∠BCD+∠D+∠DAB=360°；理由如下：
∵在△ABC和△ACD中，∠BAC+∠B+∠ACB=180°，∠DAC+∠ACD+∠D=180°，
∴∠BAC+∠B+∠ACB+∠DAC+∠ACD+∠D=2×180°=360°，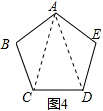
即∠ABC+∠BCD+∠D+∠DAB=360°；
（2）∠BAE+∠B+∠BCD+∠CDE+∠E=540°；理由如下：
连接AC、AD，如图4所示：
∵在△ABC、△ACD、△ADE中，∠BAC+∠B+∠ACB=180°，∠DAC+∠ACD+∠ADC=180°，∠DAE+∠ADE+∠E=180°，
∴∠BAC+∠B+∠ACB+∠DAC+∠ACD+∠ADC+∠DAE+∠ADE+∠E=3×180°=540°，
即∠BAE+∠B+∠BCD+∠CDE+∠E=540°；
（3）∠A+∠B+…∠E+∠R=（n-2）×180°；理由如下：
∵在△ABC中，∠A+∠B+∠C=180°=（3-2）×180°，
在四边形ABCD中，∠ABC+∠BCD+∠D+∠DAB=360°=（4-2）×180°，
在五边形ABCDE中，∠A+∠B+∠C+∠D+∠E=540°=（5-2）×180°，
∴在n边形ABCDE…R中，∠A+∠B+…∠E+∠R=（n-2）×180°．

点评 本题是三角形综合题目，考查了平行线的性质、三角形的内角和定理的证明以及运用等知识；熟练掌握三角形内角和定理是解决问题的关键．