题目内容
11. 如图,一次函数$y=-\frac{2}{3}x+2$的图象分别与x轴、y轴交于A、B,已线段AB为边在第一象限内作等腰Rt△ABC,使∠BAC=90°.
如图,一次函数$y=-\frac{2}{3}x+2$的图象分别与x轴、y轴交于A、B,已线段AB为边在第一象限内作等腰Rt△ABC,使∠BAC=90°.(1)分别求点A、C的坐标;
(2)在x轴上求一点P,使它到B、C两点的距离之和最小.
分析 (1)作CD⊥x轴,易证∠OAB=∠ACD,即可证明△ABO≌△CAD,可得AD=OB,CD=OA,即可解题;
(2)作C点关于x轴对称点E,连接BE,即可求得E点坐标,根据点P在直线BE上即可求得点P坐标,即可解题.
解答 解:(1)作CD⊥x轴,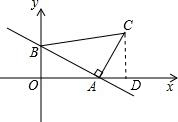
∵∠OAB+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠OAB=∠ACD,
在△ABO和△CAD中,
$\left\{\begin{array}{l}{∠AOB=∠CDA=90°}\\{∠OAB=∠ACD}\\{AB=AC}\end{array}\right.$,
∴△ABO≌△CAD(AAS)
∴AD=OB,CD=OA,
∵y=-$\frac{2}{3}$x+2与x轴、y轴交于点A、B,
∴A(3,0),B(0,2),
∴点C坐标为(5,3);
(2)作C点关于x轴对称点E,连接BE,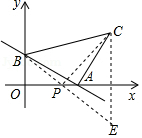
则E点坐标为(5,-3),将(0,2)(5,-3),代入y=ax+c中,
$\left\{\begin{array}{l}{5a+c=-3}\\{c=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{c=2}\end{array}\right.$
∴直线BE解析式为y=-x+2,
设点P坐标为(x,0),
则(x,0)位于直线BE上,
∴点P坐标为(2,0).
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABO≌△CAD是解题的关键.

练习册系列答案
相关题目
1.某娱乐场所组织一个翻奖牌游戏,数字的背面写有祝福语或奖金数.游戏规则是:每次翻动正面一个数字,看看背面对应的内容,就可以知道是得奖还是得到温馨祝福.请你回答下列问题:
(1)翻到奖金50元的概率是多少?
(2)翻到祝福身体健康的概率是多少?
(3)翻不到奖金的概率是多少?
正面
背面.
(1)翻到奖金50元的概率是多少?
(2)翻到祝福身体健康的概率是多少?
(3)翻不到奖金的概率是多少?
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 祝你 开心 | 奖金100元 | 学习 进步 |
| 身体 健康 | 奖金 50元 | 身体 健康 |
| 奖金 10元 | 生活 愉快 | 奖金 10元 |
6.某商场销售A、B两种品牌的洗衣机,进价及售价如表:
用45000元购进A、B两种品牌的洗衣机,全部售完后获利9600元,求商场购进A、B两种洗衣机的数量.
| 品牌 | A | B |
| 进价(元/台) | 1500 | 1800 |
| 售价(元/台) | 1800 | 2200 |
1.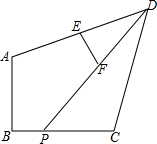 如图,已知四边形ABCD中,∠B=90°,P是BC上的动点,E,F分别是AD,DP的中点,当点P在BC上从C向B移动时,那么下列结论成立的是( )
如图,已知四边形ABCD中,∠B=90°,P是BC上的动点,E,F分别是AD,DP的中点,当点P在BC上从C向B移动时,那么下列结论成立的是( )
 如图,已知四边形ABCD中,∠B=90°,P是BC上的动点,E,F分别是AD,DP的中点,当点P在BC上从C向B移动时,那么下列结论成立的是( )
如图,已知四边形ABCD中,∠B=90°,P是BC上的动点,E,F分别是AD,DP的中点,当点P在BC上从C向B移动时,那么下列结论成立的是( )| A. | 线段EF的长先减小后增大 | B. | 线段EF的长逐渐减小 | ||
| C. | 线段EF的长不变 | D. | 线段EF的长逐渐增大 |

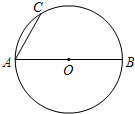 如图,AB是⊙O的直径,AC是弦.
如图,AB是⊙O的直径,AC是弦.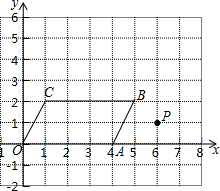 在平面直角坐标系内有一平行四边形点O(0,0),A(4,0),B(5,2),C(1,2),有一次函数y=kx+b的图象过点P(6,1).
在平面直角坐标系内有一平行四边形点O(0,0),A(4,0),B(5,2),C(1,2),有一次函数y=kx+b的图象过点P(6,1).