题目内容
14．
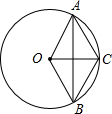如图，AB为圆O上两点，∠AOB=120°，且C为弧AB的中点，求证：AB与OC互相垂直平分．
分析 证明OA=AC=BC=OB，得到四边形AOBC是菱形，推出AB与OC互相垂直平分．
解答 证明：∵∠AOB=120°，C是AB弧的中点，
∴∠AOC=∠BOC=60°，
∵OA=OC，
∴△ACO是等边三角形，
∴OA=AC，同理OB=BC，
∴OA=AC=BC=OB，
∴四边形AOBC是菱形，
∴AB与OC互相垂直平分．
点评 本题考查圆心角、弧、弦的关系，证明菱形的方法，三角形的边长的求法，考查逻辑推理能力．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
4．一次函数y=-5x+3的图象经过的象限是（ ）
| A． | 一、二、三象限 | B． | 二、三、四象限 | C． | 一、二、四象限 | D． | 一、三、四象限 |
6．
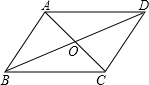如图，AC，BD是平行四边形ABCD的对角线，AC与BD交于点O，若AC=4，BD=5，BC=3，则△BOC的周长是（ ）
如图，AC，BD是平行四边形ABCD的对角线，AC与BD交于点O，若AC=4，BD=5，BC=3，则△BOC的周长是（ ）| A． | 7.5 | B． | 6 | C． | 12 | D． | 10 |
