题目内容
如图1,四边形ABCD是正方形,G是CD边上的一个动点(与C,D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.
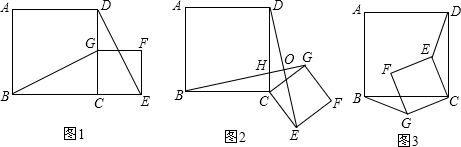
(1)猜想图1中线段BG,DE的数量关系及所在直线的位置关系(不必证明);
(2)将图1中的正方形CEFG绕点C按顺时针(或逆时针)方向任意旋转角度α;得到图2,图3.请你通过观察、测量等方法判断(1)中所得到的结论是否仍然成立,并选取图2证明你的判断.

(1)猜想图1中线段BG,DE的数量关系及所在直线的位置关系(不必证明);
(2)将图1中的正方形CEFG绕点C按顺时针(或逆时针)方向任意旋转角度α;得到图2,图3.请你通过观察、测量等方法判断(1)中所得到的结论是否仍然成立,并选取图2证明你的判断.
考点:正方形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)根据全等三角形结合图形判断出BG和DE相等且互相垂直;
(2)根据正方形的性质可得BC=CD,CE=CG,∠BCD=∠ECG=90°,然后求出∠BCG=∠DCE,再利用“边角边”证明△BCG和△DCE全等,根据全等三角形对应边相等可得BG=DE,全等三角形对应角相等可得∠CBG=∠CDE,然后求出∠DOH=90°,再根据垂直的定义证明即可.
(2)根据正方形的性质可得BC=CD,CE=CG,∠BCD=∠ECG=90°,然后求出∠BCG=∠DCE,再利用“边角边”证明△BCG和△DCE全等,根据全等三角形对应边相等可得BG=DE,全等三角形对应角相等可得∠CBG=∠CDE,然后求出∠DOH=90°,再根据垂直的定义证明即可.
解答:(1)解:BG=DE,BG⊥DE;
(2)证明:∵四边形ABCD是正方形,四边形CEFG是正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCD+∠DCG=∠ECG+∠DCG,
即∠BCG=∠DCE,
在△BCG和△DCE中,
,
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
∵∠CBG+∠BHC=90°,∠BHC=∠DHO(对顶角相等),
∴∠CDE+∠DHO=90°,
在△DHO中,∠DOH=180°-(∠CDE+∠DHO)=180°-90°=90°,
∴BG⊥DE.
(2)证明:∵四边形ABCD是正方形,四边形CEFG是正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCD+∠DCG=∠ECG+∠DCG,
即∠BCG=∠DCE,
在△BCG和△DCE中,
|
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
∵∠CBG+∠BHC=90°,∠BHC=∠DHO(对顶角相等),
∴∠CDE+∠DHO=90°,
在△DHO中,∠DOH=180°-(∠CDE+∠DHO)=180°-90°=90°,
∴BG⊥DE.
点评:本题考查了正方形的性质,全等三角形的判定与性质,熟记性质并准确识图确定出三角形全等的条件是解题的关键,也是本题的难点.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
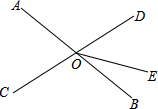 如图,直线AB,CD相交于O,已知∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE.
如图,直线AB,CD相交于O,已知∠AOC=75°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE. 如图,一个长度为8m的梯子AB的顶点A向点C滑动过程中,梯子的两端A,B与墙的底端C构成的三角形的外心与点C的距离是否发生变化?若发生变化,请说明理由;若不发生变化,求出其长度.
如图,一个长度为8m的梯子AB的顶点A向点C滑动过程中,梯子的两端A,B与墙的底端C构成的三角形的外心与点C的距离是否发生变化?若发生变化,请说明理由;若不发生变化,求出其长度. 如图,∠CPA=∠A+∠B+∠C成立吗?说明理由.
如图,∠CPA=∠A+∠B+∠C成立吗?说明理由.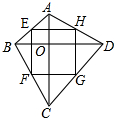 如图,四边形ABCD的对角线AC⊥BD,垂足为O,点E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是矩形.
如图,四边形ABCD的对角线AC⊥BD,垂足为O,点E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是矩形. 如图,直线AB,CD相交.求证:AB,CD只有一个交点.证明:假设AB,CD交于两点O与O′,那么过O,O′两点就有
如图,直线AB,CD相交.求证:AB,CD只有一个交点.证明:假设AB,CD交于两点O与O′,那么过O,O′两点就有