题目内容
7. 在长方形ABCD中,AB=30cm,BC=40cm,如图,P为BC上一点,PQ⊥AC,PR⊥BD,求PQ+PR的值.
在长方形ABCD中,AB=30cm,BC=40cm,如图,P为BC上一点,PQ⊥AC,PR⊥BD,求PQ+PR的值.
分析 连接OP,则三角形OBC的面积就等于长方形的面积的$\frac{1}{4}$,又由S△OPB+S△OPC=S△OBC,且OB=OC=$\frac{1}{2}$DB,于是求出DB的长度,问题即可迎刃而解.
解答 解:连接OP,如图所示:
∵ 长方形的面积=40×30=1200(cm2),
长方形的面积=40×30=1200(cm2),
∴△OBC的面积=$\frac{1}{4}$×1200=300(cm2),
又∵DB2=302+402=2500,
∴DB=50(cm),
∴OB=OC=$\frac{1}{2}$DB=25(cm),
∴$\frac{1}{2}$×25×PR+$\frac{1}{2}$×25×PQ=300,
即$\frac{1}{2}$×25×(PR+PQ)=300,
∴PR+PQ=24(cm).
点评 本题考查了矩形的性质以及面积的计算;解答此题的关键是明确△OBC的面积=长方形的面积的$\frac{1}{4}$,求出DB的长度,弄清各个三角形之间的面积关系.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
8.在下面所画的数轴中,你认为正确的数轴是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
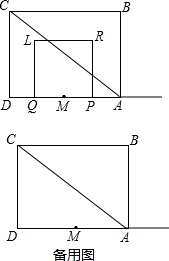 如图,四边形ABCD为矩形,AC为对角线,AB=6,BC=8,点M是AD的中点,P、Q两点同时从点M出发,点P沿射线MA向右运动;点Q沿线段MD先向左运动至点D后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与△ABC重叠部分的面积为S.
如图,四边形ABCD为矩形,AC为对角线,AB=6,BC=8,点M是AD的中点,P、Q两点同时从点M出发,点P沿射线MA向右运动;点Q沿线段MD先向左运动至点D后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与△ABC重叠部分的面积为S.