Question

11．定义：我们把对角线互相垂直的四边形叫做和美四边形，对角线交点称为和美四边形的中心．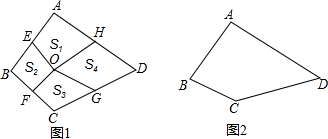

（1）写出一种你学过的和美四边形正方形；
（2）顺次连接和美四边形四边中点所得四边形是A．
A．矩形   B．菱形   C．正方形   D．无法确定
（3）如图1，点O是和美四边形ABCD的中心，E、F、G、H分别是边AB、BC、CD、DA的中点，连接OE、OF、OG、OH，记四边形AEOH、BEOF、CGOF、DHOG的面积为S₁、S₂、S₃、S₄，用等式表示S₁、S₂、S₃、S₄的数量关系（无需说明理由）
（4）如图2，四边形ABCD是和美四边形，若AB=3，BC=2，CD=4，求AD的长．

Answer 1

分析 （1）根据正方形的对角线互相垂直解答；
（2）根据矩形的判定定理解答；
（3）根据三角形的中线把三角形分为面积相等的两部分解答；
（4）根据和美四边形的定义、勾股定理计算即可．

解答 解：（1）正方形是学过的和美四边形，
故答案为：正方形；
（2）顺次连接和美四边形四边中点所得四边形是矩形，
故选：A．
（3）由和美四边形的定义可知，AC⊥BD，
则∠AOB=∠BOC=∠COD=∠DOA=90°，又E、F、G、H分别是边AB、BC、CD、DA的中点，
∴△AOE的面积=△BOE的面积，△BOF的面积=△COF的面积，△COG的面积=△DOG的面积，△DOH的面积=△AOH的面积，
∴S₁+S₃=△AOE的面积+△COF的面积+△COG的面积+△AOH的面积=S₂+S₄；
（4）如图2，连接AC、BD交于点O，则AC⊥BD，
∵在Rt△AOB中，AO²=AB²-BO²，Rt△DOC中，DO²=DC²-CO²，AB=3，BC=2，CD=4，
∴可得AD²=AO²+DO²=AB²-BO²+DC²-CO²=AB²+DC²-BC²=3²+4²-2²=21，
即可得AD=$\sqrt{21}$．

点评 本题考查的是和美四边形的定义、矩形的判定、勾股定理的应用，正确理解和美四边形的定义、掌握矩形的判定定理是解题的关键．