题目内容
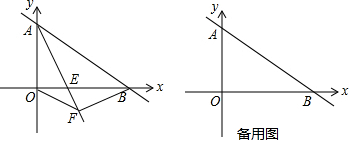
16.已知一次函数y=-$\frac{3}{4}$x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.(1)求直线AE的表达式;
(2)过点B作BF⊥AE,垂足为F,求线段BF的长度.
(3)若将已知条件“AE平分∠BAO,交x轴于点E”改变为“点E是线段OB上的一个动点(点E不与点O、B重合)”,过点B作BF⊥AE,垂足为F.设OE=x,BF=y,试求y与x之间的函数关系式,并写出函数的定义域.
分析 (1)如图1中,设OE=x,作EM⊥AB于M.首先证明△AEO≌△AEM,推出AM=AO=6,由OA=6,OB=8,∠AOB=90°,推出AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,推出BM=4,在Rt△EBM中,根据EM2+BM2=EB2,可得x2+42=(8-x)2,解方程即可.
(2)根据S△AEB=$\frac{1}{2}$•EB•OA=$\frac{1}{2}$•AE•BF,即可解决问题.
(3)利用面积即可解决,方法类似(2).
解答 解:(1)如图1中,
∵一次函数y=-$\frac{3}{4}$x+6的图象与坐标轴交于A、B点,
∴A(0,6),B(8,0),设OE=x,作EM⊥AB于M.
∵AE平分∠OAB,OE⊥OA,
∴OE=EM=x,
在△AEO和△AEM中,
$\left\{\begin{array}{l}{AE=AE}\\{OE=EM}\end{array}\right.$,
∴△AEO≌△AEM,
∴AM=AO=6,
∵OA=6,OB=8,∠AOB=90°,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴BM=4,
在Rt△EBM中,∵EM2+BM2=EB2,
∴x2+42=(8-x)2,
∴x=3,
∴E(3,0),
设直线AE的解析式为y=kx+b则$\left\{\begin{array}{l}{b=6}\\{3k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$,
∴直线AE的解析式为y=-2x+6.
(2)由(1)可知OE=3,AE=$\sqrt{O{A}^{2}+O{E}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,EB=5,
∵S△AEB=$\frac{1}{2}$•EB•OA=$\frac{1}{2}$•AE•BF,
∴BF=$\frac{5×6}{3\sqrt{5}}$=2$\sqrt{5}$.
(3)如图2中,
在Rt△AOE中,OA2+OE2=AE2,
∴AE=$\sqrt{36+{x}^{2}}$,
∵S△AEB=$\frac{1}{2}$•EB•OA=$\frac{1}{2}$•AE•BF,
∴BF=$\frac{EB•OA}{AE}$=$\frac{6(8-x)}{\sqrt{36+{x}^{2}}}$,
∴y=$\frac{48-6x}{\sqrt{36+{x}^{2}}}$(0<x<8).
点评 本题考查一次函数综合题、全等三角形的判定和性质、三角形的面积.勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用面积法求高,属于中考常考题型.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案 如图,直线AB和CD交于O点,EO⊥CD,∠EOB=47°,则∠AOC=43 度.
如图,直线AB和CD交于O点,EO⊥CD,∠EOB=47°,则∠AOC=43 度. 如图,在△ABC中,AD是角平分线,∠B=70°,∠BAC=60°,则∠ADC=100度.
如图,在△ABC中,AD是角平分线,∠B=70°,∠BAC=60°,则∠ADC=100度.