Question

2．如图，在△ABC中，∠BAC=90°，AB=AC，D、E是BC上的两点，且满足∠DAE=45°．
（1）求证：BD+EC＞DE；
（2）若BD=2，EC=4，求DE的长．

Answer 1

分析 根据翻折变换的性质易得△AFD≌△ABD；根据SAS可证△AFE≌△ACE；根据全等三角形的性质可得：BD+EC=DF+FE＞DE，∠DFE=∠DFA+∠EFA=∠B+∠C=90°，根据勾股定理进行计算即可．

解答 解：（1）把△ABD沿着AD折叠，得到△ADF，连接EF，则△AFD≌△ABD，
∴AB=AF，BD=FD，∠B=∠DFA，∠BAD=∠FAD，
∵AB=AC，
∴AF=AC，
∵∠DAE=45°，
∴∠BAD+∠CAE=45°，∠FAD+∠FAE=45°，
∴∠FAE=∠CAE，
在△AFE与△ACE中，
$\left\{\begin{array}{l}{AF=AC\\;}\\{∠FAE=∠CAE}\\{AE=AE}\end{array}\right.$，
∴△AFE≌△ACE，
∴EF=EC，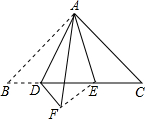
∵△DEF中，DF+EF＞DE，
∴BD+EC＞DE；

（2）∵△AFE≌△ACE，
∴∠AFE=∠C=45°，
又∵∠AFD=∠B=45°，
∴∠DFE=∠DFA+∠EFA=∠B+∠C=90°，
即△DEF是直角三角形，
∴DE=$\sqrt{D{F}^{2}+E{F}^{2}}$，
又∵DF=BD=2，EF=EC=4，
∴DE=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$．

点评 本题主要考查了全等三角形的判定与性质、等腰直角三角形的性质以及三角形的三边关系的综合应用，根据翻折变换证得△AFD≌△ABD和△AFE≌△ACE是解题的关键．本题也可以运用旋转变换进行求解．