题目内容
19.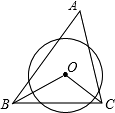 如图,在三角形ABC中,∠A=70°,⊙O截△ABC的三边所得的弦相等,则∠BOC=125°.
如图,在三角形ABC中,∠A=70°,⊙O截△ABC的三边所得的弦相等,则∠BOC=125°.
分析 根据弦相等,则对应的弦心距相等,即O到△ABC的三边相等,则O是△ABC的内心,然后根据内心的性质求解.
解答 解:∵⊙O截△ABC的三边所得的弦相等,
∴O到△ABC三边的距离相等,
∴O在三角形的角的平分线上,即O是△ABC的内心.
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB),
又∵△ABC中,∠ABC+∠ACB=180°-∠A=180°-70°=110°.
∴∠OBC+∠OCB=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
故答案是:125°.
点评 本题考查了三角形的内心,以及圆的性质,正确证明O是△ABC的内心是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.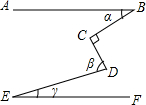 如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
 如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )| A. | ∠β=∠α+∠γ | B. | ∠α+∠β+∠γ=180° | C. | ∠α+∠β-∠γ=90° | D. | ∠β+∠γ-∠α=90° |
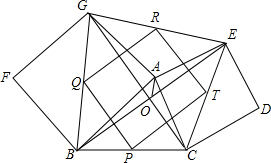 如图,已知△ABC,分别以AB,AC为边作正方形ABFG和正方形ACDE,连接BE,CG交于点O,联结AO,P、Q、R、T分别是BC、BG、EG、CE的中点.
如图,已知△ABC,分别以AB,AC为边作正方形ABFG和正方形ACDE,连接BE,CG交于点O,联结AO,P、Q、R、T分别是BC、BG、EG、CE的中点.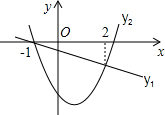 已知函数y1=px+q和y2=ax2+bx+c的图象如图所示,看图回答:
已知函数y1=px+q和y2=ax2+bx+c的图象如图所示,看图回答: