题目内容
14.已知三角形两边长分别为2和4,第三边是方程x2-4x+3=0的解,则这个三角形的周长是9.分析 先解方程求出方程的解,根据三角形的三边关系定理判断能否组成三角形,最后求出即可.
解答 解:x2-4x+3=0,
解方程得:x=3或1,
当三角形的三边为1,2,4时,不符合三角形的三边关系定理,此时三角形不存在;
当三角形的三边为3,2,4时,符合三角形的三边关系定理,此时三角形的周长为3+2+4=9,
故答案为:9.
点评 本题考查了解一元二次方程,三角形的三边关系定理的应用,能求出一元二次方程的解是解此题的关键,注意:解一元二次方程的方法有:直接开平方法,公式法,因式分解法,配方法.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
5.在下列命题中,正确的是( )
| A. | 正多边形一个内角与一个外角相等,则它是正六边形 | |
| B. | 正多边形都是中心对称图形 | |
| C. | 边数大于3的正多边形的对角线长都相等 | |
| D. | 正多边形的一个外角为36°,则它是正十边形 |
3.一次函数y=kx+b(k>0,b>0)的图象经过( )
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
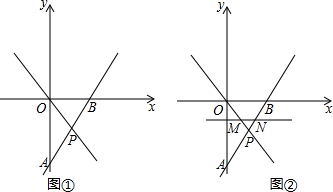
 如图,已知AB=AC,BE=CD,∠B=∠C,则△ABD≌ACE,根据是SAS.
如图,已知AB=AC,BE=CD,∠B=∠C,则△ABD≌ACE,根据是SAS.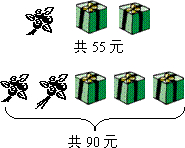 母亲节那天,很多同学给妈妈准备了鲜花和礼盒.
母亲节那天,很多同学给妈妈准备了鲜花和礼盒.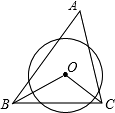 如图,在三角形ABC中,∠A=70°,⊙O截△ABC的三边所得的弦相等,则∠BOC=125°.
如图,在三角形ABC中,∠A=70°,⊙O截△ABC的三边所得的弦相等,则∠BOC=125°.