题目内容
已知关于x的一元二次方程2x2+4x+k-1=0有实数根,k为正整数.
(1)求k的值
(2)当此方程有两个非零的整数根时,将关于x的二次函数y=2x2+4x+k-1的图象向右平移1个单位,向下平移2个单位,求平移后的图象的解析式.
(1)求k的值
(2)当此方程有两个非零的整数根时,将关于x的二次函数y=2x2+4x+k-1的图象向右平移1个单位,向下平移2个单位,求平移后的图象的解析式.
考点:根的判别式,二次函数图象与几何变换
专题:
分析:(1)根据一元二次方程2x2+4x+k-1=0有实数根,可推△≥0,求出k≤3.又因为k为正整数,可确定k=1或2或3.
(2)分别把k=1或2或3代入方程2x2+4x+k-1=0,解得结果进行分析,只有x=-1为所求,进一步将关于x的二次函数y=2x2+4x+k-1的图象向右平移1个单位,向下平移2个单位,得出函数解析式即可.
(2)分别把k=1或2或3代入方程2x2+4x+k-1=0,解得结果进行分析,只有x=-1为所求,进一步将关于x的二次函数y=2x2+4x+k-1的图象向右平移1个单位,向下平移2个单位,得出函数解析式即可.
解答:解:(1)∵方程2x2+4x+k-1=0有实数根,
∴△=42-4×2×(k-1)≥0,
∴k≤3.
又∵k为正整数,
∴k=1或2或3.
(2)当此方程有两个非零的整数根时,
当k=1时,方程为2x2+4x=0,解得x1=0,x2=-2;不合题意,舍去.
当k=2时,方程为2x2+4x+1=0,解得x1=-1+
,x2=-1-
;不合题意,舍去.
当k=3时,方程为2x2+4x+2=0,解得x1=x2=-1;符合题意.
因此y=2x2+4x+2的图象向右平移1个单位,向下平移2个单位,得出y=2x2-2.
∴△=42-4×2×(k-1)≥0,
∴k≤3.
又∵k为正整数,
∴k=1或2或3.
(2)当此方程有两个非零的整数根时,
当k=1时,方程为2x2+4x=0,解得x1=0,x2=-2;不合题意,舍去.
当k=2时,方程为2x2+4x+1=0,解得x1=-1+
| ||
| 2 |
| ||
| 2 |
当k=3时,方程为2x2+4x+2=0,解得x1=x2=-1;符合题意.
因此y=2x2+4x+2的图象向右平移1个单位,向下平移2个单位,得出y=2x2-2.
点评:此题考查了一元二次方程根的判别式和二次函数平移的性质,求得方程的整数根是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法错误的是( )
| A、抛掷一枚硬币,硬币落地时正面朝上是随机事件 |
| B、把4个球随机放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 |
| C、方程x2+x-2=0的两个根是1和-2是不可能事件 |
| D、一个盒子中有白球m个,红球6个,黑球n个(每个球除了颜色外都相同),如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是6 |
关于函数y=
,下列说法正确的是( )
| 2 |
| x |
| A、函数图象关于原点对称 |
| B、函数图象关于x轴对称 |
| C、函数图象关于y轴对称 |
| D、y的值随x值的增大而减小 |
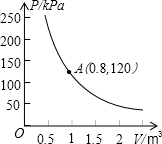 某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气体的气压大于150kPa时,气球将爆炸.为了安全,气体体积V应该是( )
某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气体的气压大于150kPa时,气球将爆炸.为了安全,气体体积V应该是( )| A、小于0.64m3 |
| B、大于0.64m3 |
| C、不小于0.64m3 |
| D、不大于0.64m3 |
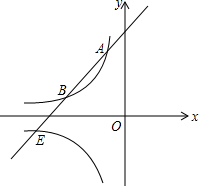 如图,已知直线y=ax+b过A(-1,6)与双曲线y=
如图,已知直线y=ax+b过A(-1,6)与双曲线y=