题目内容
某校一间宿舍里有若干名学生,其中一人担任舍长.元旦时,该宿舍里的每名学生互赠一张贺卡,并且每人又赠给宿舍楼的每位管理员一张贺卡,每位宿舍管理员也回赠舍长一张贺卡,这样共用去了51张贺卡,问这间宿舍里住有多少名学生和管理员?
考点:一元二次方程的应用
专题:
分析:设有x个学生,y个管理员.
①该宿舍每位学生与赠一张贺卡,那么每个人收到的贺卡就是x-1张,那么总共就用去了x(x-1)(乘法原理)张贺卡;
②每个人又赠给每一位管理员一张贺卡,那么就用去了xy(乘法原理)张贺卡;
③每位管理员也回赠舍长一张贺卡,那么就用去了y张贺卡;
所以根据题意列出方程:x(x-1)+xy+y=51(加法原理),然后根据生活实际情况解方程即可.
①该宿舍每位学生与赠一张贺卡,那么每个人收到的贺卡就是x-1张,那么总共就用去了x(x-1)(乘法原理)张贺卡;
②每个人又赠给每一位管理员一张贺卡,那么就用去了xy(乘法原理)张贺卡;
③每位管理员也回赠舍长一张贺卡,那么就用去了y张贺卡;
所以根据题意列出方程:x(x-1)+xy+y=51(加法原理),然后根据生活实际情况解方程即可.
解答:解:设有x个学生,y个管理员.
该宿舍每位学生与赠一张贺卡,那么每个人收到的贺卡就是x-1张,那么总共就用去了x(x-1)张贺卡;
每个人又赠给每一位管理员一张贺卡,那么就用去了xy张贺卡;
每位管理员也回赠舍长一张贺卡,那么就用去了y张贺卡;
∴x(x-1)+xy+y=51,
∴51=x(x-1)+xy+y=x(x-1)+y(x+1)≥x(x-1)+x+1=x2+1(当y=1时取“=”),
解得x≤7;
x(x-1)+(x+1)y=51
∵51是奇数,而x和x-1中,有一个是偶数,
∴x(x-1)是偶数,
∴(x+1)y是奇数,
∴x是偶数,
而x≤7,所以x只有2 4 6三种情况;
当x=2时,y=
(不是整数,舍去);
当x=4时,y=
(不是整数,舍去);
当x=6时,y=3.
所以这个宿舍有6个学生.
该宿舍每位学生与赠一张贺卡,那么每个人收到的贺卡就是x-1张,那么总共就用去了x(x-1)张贺卡;
每个人又赠给每一位管理员一张贺卡,那么就用去了xy张贺卡;
每位管理员也回赠舍长一张贺卡,那么就用去了y张贺卡;
∴x(x-1)+xy+y=51,
∴51=x(x-1)+xy+y=x(x-1)+y(x+1)≥x(x-1)+x+1=x2+1(当y=1时取“=”),
解得x≤7;
x(x-1)+(x+1)y=51
∵51是奇数,而x和x-1中,有一个是偶数,
∴x(x-1)是偶数,
∴(x+1)y是奇数,
∴x是偶数,
而x≤7,所以x只有2 4 6三种情况;
当x=2时,y=
| 49 |
| 3 |
当x=4时,y=
| 39 |
| 5 |
当x=6时,y=3.
所以这个宿舍有6个学生.
点评:本题主要考查了加法原理和乘法原理.解答此题的难点是根据实际情况解方程x(x-1)+(x+1)y=51,解该方程利用了奇数与偶数的知识.

练习册系列答案
相关题目
方程x2=x的解是( )
| A、0 | B、1 | C、无解 | D、0和1 |
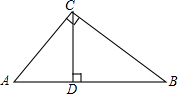 如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AC=3,BC=4,求AD的长.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AC=3,BC=4,求AD的长.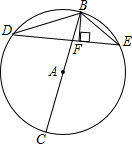 如图,BC是⊙A的直径,△DBE的各个顶点在⊙A上,BF⊥DE于点F.求证:BD•BE=BC•BF.
如图,BC是⊙A的直径,△DBE的各个顶点在⊙A上,BF⊥DE于点F.求证:BD•BE=BC•BF.