题目内容
16.计算:(1)$\frac{\sqrt{21}×\sqrt{7}}{\sqrt{3}}$-(1-$\sqrt{5}$)0;
(2)3$\sqrt{40}$-$\sqrt{\frac{2}{5}}$-2$\sqrt{\frac{1}{10}}$.
分析 (1)先根据二次根式的除法法则和零指数幂的意义计算,然后进行减法运算;
(2)先把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=$\sqrt{\frac{21×7}{3}}$-1
=7-1
=6;
(2)原式=6$\sqrt{10}$-$\frac{\sqrt{10}}{5}$-$\frac{\sqrt{10}}{5}$
=$\frac{28\sqrt{10}}{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | $\sqrt{-16}$=-4 | B. | $\sqrt{16}$=±4 | C. | $\sqrt{(-4)^{2}}$=-4 | D. | $\root{3}{(-4)^{3}}$=-4 |
8.下列二次三项式中,在实数范围内不能因式分解的是( )
| A. | 6x2+x-15 | B. | 3y2+7y+3 | C. | x2+4x+4 | D. | 2x2-4x+5 |
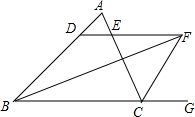 如图,在△ABC中,已知∠ABC和△ABC的外角∠ACG的平分线交于点F,过点F作FD∥BC,FD分别交AB、AC于点D、E,求证:DE=BD-CE.
如图,在△ABC中,已知∠ABC和△ABC的外角∠ACG的平分线交于点F,过点F作FD∥BC,FD分别交AB、AC于点D、E,求证:DE=BD-CE.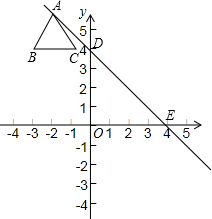 在平面直角坐标系中,直线y=kx+b经过两点D(0,4),E(4,0),边长为2个单位长度的等边△ABC,顶点A在该直线上滑动,在滑动过程中始终保持边BC∥x轴,且顶点A在BC的上方.
在平面直角坐标系中,直线y=kx+b经过两点D(0,4),E(4,0),边长为2个单位长度的等边△ABC,顶点A在该直线上滑动,在滑动过程中始终保持边BC∥x轴,且顶点A在BC的上方.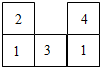 图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.
图中是由几个小立方块搭成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的从正面看和从左面看的形状图.