题目内容
6.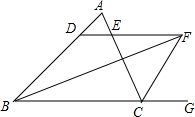 如图,在△ABC中,已知∠ABC和△ABC的外角∠ACG的平分线交于点F,过点F作FD∥BC,FD分别交AB、AC于点D、E,求证:DE=BD-CE.
如图,在△ABC中,已知∠ABC和△ABC的外角∠ACG的平分线交于点F,过点F作FD∥BC,FD分别交AB、AC于点D、E,求证:DE=BD-CE.
分析 证明BD=FD,CE=FE,即可解决问题.
解答 证明:∵∠ABC的平分线和外角∠ACF的平分线交于点F,
∴∠DBF=∠CBF,∠ECF=∠GCF;
∵FD∥BC,
∴∠DFB=∠CBF,∠EFC=∠GCF,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴BD=FD,EC=EF;
∴DE=BD-CE
点评 该题主要考查了等腰三角形的判定、平行线的性质等几何知识点的应用问题;牢固掌握等腰三角形的判定、平行线的性质等几何知识点是灵活运用、解题的基础和关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.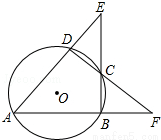 如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
 如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )| A. | α+β | B. | $\frac{α+β}{2}$ | C. | 180°-α-β | D. | $\frac{180°-α-β}{2}$ |
11.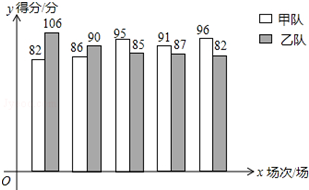 甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
(1)请根据统计图填写下表
(2)如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、方差以及获胜场数这三个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
 甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)(1)请根据统计图填写下表
| 平均数 | 中位数 | 方差 | |
| 甲 | 90 | 91 | 28.4 |
| 乙 | 90 | 87 | 70.8 |
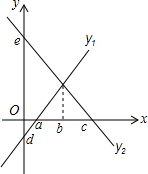 如图,先观察图形,然后填空:
如图,先观察图形,然后填空: