题目内容
8.下列二次三项式中,在实数范围内不能因式分解的是( )| A. | 6x2+x-15 | B. | 3y2+7y+3 | C. | x2+4x+4 | D. | 2x2-4x+5 |
分析 利用一元二次方程根的情况决定二次三项式的因式分解,进而分析b2-4ac的符号,得出答案.
解答 解:A、6x2+x-15=0时,
b2-4ac=1+4×6×15=361>0,
则此二次三项式在实数范围内能因式分解,故此选项错误;
B、3y2+7y+3
b2-4ac=49-4×3×3=13>0,
则此二次三项式在实数范围内能因式分解,故此选项错误;
C、x2+4x+4
b2-4ac=16-4×4=0,
则此二次三项式在实数范围内能因式分解,故此选项错误;
D、2x2-4x+5
b2-4ac=16-4×2×5=--24<0,
则此二次三项式在实数范围内不能因式分解,故此选项正确.
故选:D.
点评 此题主要考查了实数范围内分解因式,正确分析b2-4ac的符号是解题关键.

练习册系列答案
相关题目
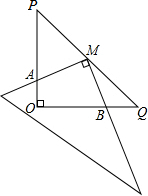 如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.