题目内容
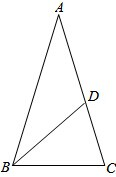 已知在△ABC中,AB=AC,∠A=36°,∠ABC的平分线BD与AC交于D,求证:BC=
已知在△ABC中,AB=AC,∠A=36°,∠ABC的平分线BD与AC交于D,求证:BC=
| ||
| 2 |
考点:黄金分割
专题:证明题
分析:根据等腰三角形的性质和三角形内角和定理得到∠ABC=∠C=72°,再利用角平分线的定义得∠ABD=
∠ABC=36°,则DA=DB,于是可证明△BDC∽△ABC,利用相似比得到CD:BC=BC:AC,利用等线段代换CD:AD=AD:AC,于是可根据黄金分割的定义得AD=
AC,即有BC=
AB.
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=
(180°-36°)=72°,
∵∠ABC的平分线BD与AC交于D,
∴∠ABD=
∠ABC=36°,
∴DA=DB,
∵∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∵∠C=∠ABC=∠BDC=72°,
∴△BDC∽△ABC,
∴CD:BC=BC:AC,
∴CD:AD=AD:AC,
∴AD=
AC,
∴BC=
AB.
∴∠ABC=∠C=
| 1 |
| 2 |
∵∠ABC的平分线BD与AC交于D,
∴∠ABD=
| 1 |
| 2 |
∴DA=DB,

∵∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∵∠C=∠ABC=∠BDC=72°,
∴△BDC∽△ABC,
∴CD:BC=BC:AC,
∴CD:AD=AD:AC,
∴AD=
| ||
| 2 |
∴BC=
| ||
| 2 |
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
相关题目
直径为8的圆内有一点M到圆心O的距离是3,则过点M的弦中,长度为整数的条数为( )
| A、3 | B、4 | C、5 | D、6 |
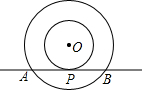 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,大圆、小圆的半径分别为10cm和6cm,则AB=
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点,大圆、小圆的半径分别为10cm和6cm,则AB=