题目内容
读句画图
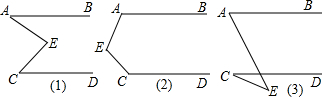
(1)画∠AOB=45°,并在∠AOB内部任意画点P;
(2)作P点关于OB的对称点P1,P点关于OA的对称点P2;
(3)探究P1,O,P2三点所构成的三角形的形状,并说明理由.
(1)画∠AOB=45°,并在∠AOB内部任意画点P;
(2)作P点关于OB的对称点P1,P点关于OA的对称点P2;
(3)探究P1,O,P2三点所构成的三角形的形状,并说明理由.
考点:作图-轴对称变换
专题:作图题
分析:(1)用三角板作出45°角即可;
(2)根据轴对称的定义分别作出P1、P2即可;
(3)连接OP,根据轴对称的性质可得OP1=OP=OP2,∠BOP1=∠BOP,∠AOP2=∠AOP,然后求出∠P1OP2=2∠AOB=90°,再根据等腰直角三角形的定义判定即可.
(2)根据轴对称的定义分别作出P1、P2即可;
(3)连接OP,根据轴对称的性质可得OP1=OP=OP2,∠BOP1=∠BOP,∠AOP2=∠AOP,然后求出∠P1OP2=2∠AOB=90°,再根据等腰直角三角形的定义判定即可.
解答: 解:(1)如图所示;
解:(1)如图所示;
(2)P点关于OB的对称点P1,P点关于OA的对称点P2如图所示;
(3)连接OP,
由轴对称的性质得,OP1=OP=OP2,∠BOP1=∠BOP,∠AOP2=∠AOP,
所以∠P1OP2=2∠AOB=90°,
所以,P1,O,P2三点所构成的三角形是等腰直角三角形.
 解:(1)如图所示;
解:(1)如图所示;(2)P点关于OB的对称点P1,P点关于OA的对称点P2如图所示;
(3)连接OP,
由轴对称的性质得,OP1=OP=OP2,∠BOP1=∠BOP,∠AOP2=∠AOP,
所以∠P1OP2=2∠AOB=90°,
所以,P1,O,P2三点所构成的三角形是等腰直角三角形.
点评:本题考查了利用轴对称变换作图,轴对称的性质,等腰直角三角形的判定,熟记性质以及轴对称点的作法是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
 如图,△ABC≌△BAD,∠C与∠D对应,AC与BD对应,AB=8cm,BD=5cm,AD=7cm,那么BC=
如图,△ABC≌△BAD,∠C与∠D对应,AC与BD对应,AB=8cm,BD=5cm,AD=7cm,那么BC= 如图,将正方形ABCD绕B点旋转a(0°<a<90°),使A′D′交DC于E点.试猜想A′E与CE的数量关系,并证明你的结论.
如图,将正方形ABCD绕B点旋转a(0°<a<90°),使A′D′交DC于E点.试猜想A′E与CE的数量关系,并证明你的结论.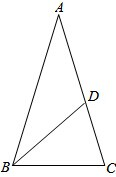 已知在△ABC中,AB=AC,∠A=36°,∠ABC的平分线BD与AC交于D,求证:BC=
已知在△ABC中,AB=AC,∠A=36°,∠ABC的平分线BD与AC交于D,求证:BC=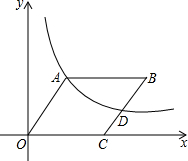 如图,在平面直角坐标坐标系中,菱形OABC的顶点C的坐标为(6,0),cos∠AOC=
如图,在平面直角坐标坐标系中,菱形OABC的顶点C的坐标为(6,0),cos∠AOC=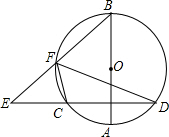 如图,⊙O中,直径AB⊥CD,E为DC延长线上一点,BF交⊙O于F.求证:∠EFC=∠BFD.
如图,⊙O中,直径AB⊥CD,E为DC延长线上一点,BF交⊙O于F.求证:∠EFC=∠BFD.