题目内容
计算:
+
+…+
.
| 1 |
| 1×2×3 |
| 1 |
| 2×3×4 |
| 1 |
| 100×101×102 |
考点:有理数的混合运算
专题:
分析:由
=
×
=
×
=
×[
-
]=
[
-
]可得到式子的规律,代入计算即可.
| 1 |
| n(n+1)(n+2) |
| 1 |
| 2 |
| 2 |
| n(n+1)(n+2) |
| 1 |
| 2 |
| n+2-n |
| n(n+1)(n+2) |
| 1 |
| 2 |
| n+2 |
| n(n+1)(n+2) |
| n |
| n(n+1)(n+2) |
| 1 |
| 2 |
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
解答:解:原式=
×(
-
)+
×(
-
)+…+
×(
-
)
=
(
-
+
-
+…+
-
)
=
×(
-
)
=
×
=
.
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 100×101 |
| 1 |
| 101×102 |
=
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 100×101 |
| 1 |
| 101×102 |
=
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 101×102 |
=
| 1 |
| 2 |
| 2575 |
| 5151 |
=
| 2575 |
| 10302 |
点评:本题主要考查有理数的混合运算,找出式子的变化规律是解题的关键.

练习册系列答案
相关题目
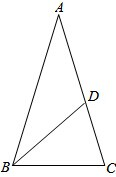 已知在△ABC中,AB=AC,∠A=36°,∠ABC的平分线BD与AC交于D,求证:BC=
已知在△ABC中,AB=AC,∠A=36°,∠ABC的平分线BD与AC交于D,求证:BC=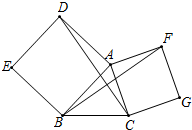 如图,以△ABC中AB、AC为边分别作正方形ADEB与ACGF,连接DC、BF.则CD与BF的数量关系是
如图,以△ABC中AB、AC为边分别作正方形ADEB与ACGF,连接DC、BF.则CD与BF的数量关系是