题目内容
直径为8的圆内有一点M到圆心O的距离是3，则过点M的弦中，长度为整数的条数为（ ）
| A、3 | B、4 | C、5 | D、6 |
考点：垂径定理,勾股定理
专题：计算题
分析：AB为过点M的直径，过M点作CD⊥AB，如图，连结OC，根据圆的有关性质得AB为过M的最长的弦，CD为过M点最短的弦，在Rt△OCM中根据勾股定理计算出CM=
，再根据垂径定理得到CM=DM=
，则CD=2
，设过M的弦的长度为a，则2
≤a≤8，确定整数a为6，7，8，利用圆的对称性易得弦长为6和7的弦各有两条，弦长为8的只有一条．
| 7 |
| 7 |
| 7 |
| 7 |
解答：解：
AB为过点M的直径，过M点作CD⊥AB，如图，连结OC，
则AB为过M的最长的弦，CD为过M点最短的弦，AB=8，
在Rt△OCM中，∵OC=4，OM=3，
∴CM=
=
，
∵OM⊥CD，
∴CM=DM=
，
∴CD=2
，
设过M的弦的长度为a，则2
≤a≤8，
∴整数a为6，7，8，
∵弦长为6和7的弦各有两条，弦长为8的只有一条，
∴过点M的弦中，长度为整数的条数为5条．
故选C．
AB为过点M的直径，过M点作CD⊥AB，如图，连结OC，则AB为过M的最长的弦，CD为过M点最短的弦，AB=8，
在Rt△OCM中，∵OC=4，OM=3，
∴CM=
| OC2-OM2 |
| 7 |
∵OM⊥CD，
∴CM=DM=
| 7 |
∴CD=2
| 7 |
设过M的弦的长度为a，则2
| 7 |
∴整数a为6，7，8，
∵弦长为6和7的弦各有两条，弦长为8的只有一条，
∴过点M的弦中，长度为整数的条数为5条．
故选C．
点评：本题考查了垂径定理：垂直弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．
练习册系列答案
相关题目
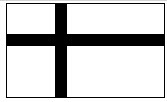如图，某中学为方便师生活动，准备在长30m、宽20m的矩形草坪上修筑两横两纵四条小路，横、纵路的宽度之比为3：2，若要使余下的草坪面积是原来草坪面积的
如图，将正方形ABCD绕B点旋转a（0°＜a＜90°），使A′D′交DC于E点．试猜想A′E与CE的数量关系，并证明你的结论．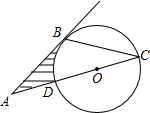
如图，AB为⊙O的切线，切点为点B，切线BA与直径CD的延长线相交于点A，CD=4，∠A=30°，则图中阴影部分的面积为
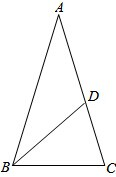已知在△ABC中，AB=AC，∠A=36°，∠ABC的平分线BD与AC交于D，求证：BC=
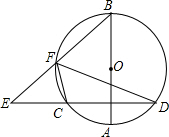如图，⊙O中，直径AB⊥CD，E为DC延长线上一点，BF交⊙O于F．求证：∠EFC=∠BFD．