题目内容
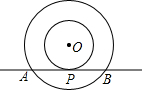如图，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，大圆、小圆的半径分别为10cm和6cm，则AB=考点：切线的性质,勾股定理,垂径定理
专题：计算题
分析：结OP、OA，如图，根据切线的性质得OP⊥AB，再根据垂径定理得到AP=BP，然后在Rt△AOP中，利用勾股定理可计算出AP=8，再利用AB=2AP进行计算即可．
解答：解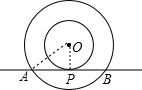
：连结OP、OA，如图，
∵大圆的弦AB是小圆的切线，点P为切点，
∴OP⊥AB，
∴AP=BP，
在Rt△AOP中，∵OP=6，OA=10，
∴AP=
=8，
∴AB=2AP=16cm．
故答案为16．
：连结OP、OA，如图，∵大圆的弦AB是小圆的切线，点P为切点，
∴OP⊥AB，
∴AP=BP，
在Rt△AOP中，∵OP=6，OA=10，
∴AP=
| OA2-OP2 |
∴AB=2AP=16cm．
故答案为16．
点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
期末集结号系列答案
相关题目
如图，在△ABC中，分别以点A和点B为圆心，大于
如图，将正方形ABCD绕B点旋转a（0°＜a＜90°），使A′D′交DC于E点．试猜想A′E与CE的数量关系，并证明你的结论．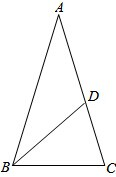
已知在△ABC中，AB=AC，∠A=36°，∠ABC的平分线BD与AC交于D，求证：BC=
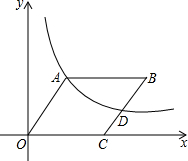如图，在平面直角坐标坐标系中，菱形OABC的顶点C的坐标为（6，0），cos∠AOC=