题目内容
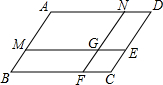 如图,在?ABCD中,点M,N分别在AB、AD上,且BM=DN.过点M作ME∥AD交CD于点E,过点N作NF∥AB交BC于点F,ME与NF相交于点G.
如图,在?ABCD中,点M,N分别在AB、AD上,且BM=DN.过点M作ME∥AD交CD于点E,过点N作NF∥AB交BC于点F,ME与NF相交于点G.求证:四边形CEGF是菱形.
考点:平行四边形的性质,菱形的判定
专题:证明题
分析:根据平行四边形的性质得出AD∥BC,AB∥CD,推出平行四边形ADEM、ABNF、GECF,求出GE=DN=GF=BM,根据菱形的判定得出即可.
解答:证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AD∥BC,AB∥CD,
∵NF∥AB,ME∥AD,
∴NF∥CD,ME∥BC,
∴四边形DNGE和四边形BMGF是平行四边形,
∴DN=EG,BM=GF,
∵BM=DN,
∴GF=GE,
∵GF∥CD,BC∥ME,
∴四边CEGF是平行四边形,
∴四边形CEGF是菱形.
∴AD=BC,AB=CD,AD∥BC,AB∥CD,
∵NF∥AB,ME∥AD,
∴NF∥CD,ME∥BC,
∴四边形DNGE和四边形BMGF是平行四边形,
∴DN=EG,BM=GF,
∵BM=DN,
∴GF=GE,
∵GF∥CD,BC∥ME,
∴四边CEGF是平行四边形,
∴四边形CEGF是菱形.
点评:本题考查了菱形的判定,平行四边形的性质和判定的应用,解题的关键是能求出平行四边形CEGF和推出GF=GE,注意:有一组邻边相等的平行四边形是菱形.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
在下列各组交通标志中,两个图形不相似的是( )
A、 |
B、 |
C、 |
D、 |
 如图,是一个铁皮制作的圆锥形烟囱帽,量得它的高OA=30cm,母线AB=50cm,则制作这样的烟囱帽(不考虑接缝)需要的铁皮面积是( )cm2.
如图,是一个铁皮制作的圆锥形烟囱帽,量得它的高OA=30cm,母线AB=50cm,则制作这样的烟囱帽(不考虑接缝)需要的铁皮面积是( )cm2.| A、1500π |
| B、1200π |
| C、2000π |
| D、4000π |
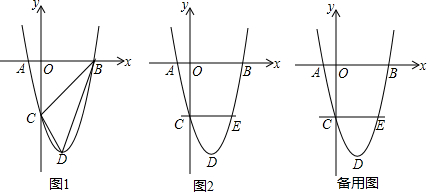
 已知:直线y=-
已知:直线y=- 如图,小明从A地沿北偏东60°方向走2千米到B地,再从B地正南方向走3千米到C地,此时小明距离A地
如图,小明从A地沿北偏东60°方向走2千米到B地,再从B地正南方向走3千米到C地,此时小明距离A地