题目内容
给定直线l:y=kx,抛物线C:y=ax2+bx+1.
(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点.
①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=P Q.
Q.
(1)解:
∵l:y=kx,C:y=ax2+bx+1,当b=1时有A,B两交点,
∴A,B两点的横坐标满足kx=ax2+x+1,即ax2+(1﹣k)x+1=0.
∵B与A关于原点对称,
∴0=xA+xB=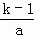 ,
,
∴k=1.
∵y=ax2+x+1=a(x+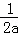 )2+1﹣
)2+1﹣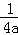 ,
,
∴顶点(﹣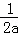 ,1﹣
,1﹣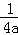 )在y=x上,
)在y=x上,
∴﹣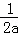 =1﹣
=1﹣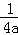 ,
,
解得 a=﹣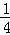 .
.
(2)
①解:∵无论非零实数k取何值,直线r与抛物线C都只有一个交点,
∴k=1时,k=2时,直线r与抛物线C都只有一个交点.
当k=1时,r:y=x+2,
∴代入C:y=ax2+bx+1中,有ax2+(b﹣1)x﹣1=0,
∵△=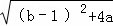 =0,
=0,
∴(b﹣1)2+4a=0,
当k=2时,r:y=2x+5,
∴代入C:y=ax2+bx+1中,有ax2+(b﹣2)x﹣4=0,
∵△=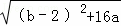 =0,
=0,
∴(b﹣2)2+16a=0,
∴联立得关于a,b的方程组 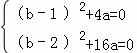 ,
,
解得 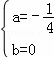 或
或  .
.
∵r:y=kx+k2+1代入C:y=ax2+bx+1,得ax2+(b﹣k)x﹣k2=0,
∴△=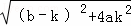 .
.
当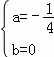 时,△=
时,△=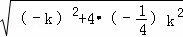 =
=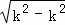 =0,故无论k取何值,直线r与抛物线C都只有一个交点.
=0,故无论k取何值,直线r与抛物线C都只有一个交点.
当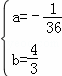 时,△=
时,△=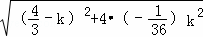 =
=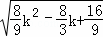 ,显然虽k值的变化,△不恒为0,所以不合题意舍去.
,显然虽k值的变化,△不恒为0,所以不合题意舍去.
∴C:y=﹣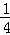 x2+1.
x2+1.
②证明:
根据题意,画出图象如图1,
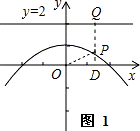
由P在抛物线y=﹣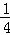 x2+1上,设P坐标为(
x2+1上,设P坐标为( x,﹣
x,﹣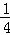 x2+
x2+ 1
1 ),连接OP,过P作PQ⊥直线y=2于Q,作PD⊥x轴于D,
),连接OP,过P作PQ⊥直线y=2于Q,作PD⊥x轴于D,
∵PD=|﹣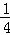 x2+1|,OD=|x|,
x2+1|,OD=|x|,
∴OP=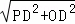 =
=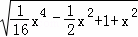 =
=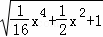 =
=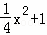 ,
,
PQ=2﹣yP=2﹣(﹣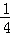 x2+1)=
x2+1)=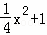 ,
,
∴OP=PQ.

 期末集结号系列答案
期末集结号系列答案二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
| X | ﹣1 | 0 | 1 | 3 |
| y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个 B. 3个 C. 2个 D. 1个
 .
.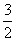 D.x=-
D.x=-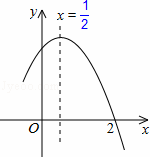
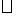 BDEF=y cm2.
BDEF=y cm2.
 铅球路线的最高处B点的坐标为
铅球路线的最高处B点的坐标为 B(6,5).
B(6,5).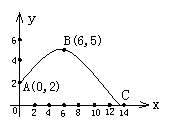
 达
达 直径 ②半圆是弧 ③长度相等的弧是等弧 ④经过圆内一点可以作无数条直径
直径 ②半圆是弧 ③长度相等的弧是等弧 ④经过圆内一点可以作无数条直径