题目内容
如图,二次函y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣2,y1),(,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
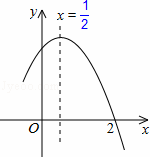
A ①②④ B ③④ C ①③④ D ①②
A

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
如图2-131所示,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在x轴的正半轴上),与y轴交于 点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC,AC上,抛物线P上的部分点的横坐标对
点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC,AC上,抛物线P上的部分点的横坐标对 应的纵坐标如下.
应的纵坐标如下.
| x | … | -3 | -2 | 1 | 2 | … |
| y | … | - | -4 | - | 0 | … |
(1)求A,B,C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并
指出m的取值范围;
(3)当矩形DEFG的面积S最 大时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围;
大时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围;
(4)若点D的坐标为(1,0),求矩形DEFG的面积.
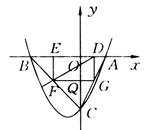

 Q.
Q.
 坐标为( ).
坐标为( ).


 cm C. 2
cm C. 2 cm D. 2
cm D. 2 cm
cm