题目内容
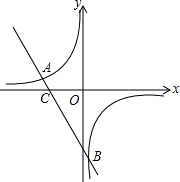 如图所示,直线y=-2x+b与反比例函数y=
如图所示,直线y=-2x+b与反比例函数y=| k |
| x |
(1)若A(-3,m)、B(1,n).直接写出不等式-2x+b>
| k |
| x |
(2)求sin∠OCB的值.
(3)若CB-CA=5,求直线AB的解析式.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)不等式的解即为函数y=-2x+b的图象在函数y=
上方的x的取值范围.可由图象直接得到.
(2)用b表示出OC和OF的长度,求出∠OCF的正切值,进而求出sin∠OCB.
(3)求直线AB的解析式关键是求出b的值.
| k |
| x |
(2)用b表示出OC和OF的长度,求出∠OCF的正切值,进而求出sin∠OCB.
(3)求直线AB的解析式关键是求出b的值.
解答:解:(1)如图:
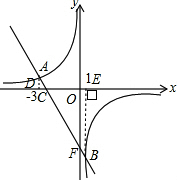
由图象得:不等式-2x+b>
的解是x<-3或0<x<1;
(2)设直线AB和y轴的交点为F.
当y=0时,x=
,即OC=-
当x=0时,y=b,即OF=-b
∴tan∠OCB=
=2
∴sin∠OCB=
=
.
(3)过A作AD⊥x轴,过B作BE⊥x轴
则AC=
AD=
yA
BC=
BE=-
yB
∴AC-BC=
(yA+yB)=-
(xA+xB)+
b=-5,
又-2x+b=
所以-2x2+bx-k=0
∴xA+xB=
∴-
×
+
b=-5
∴b=-2
∴y=-2x-2
.

由图象得:不等式-2x+b>
| k |
| x |
(2)设直线AB和y轴的交点为F.
当y=0时,x=
| b |
| 2 |
| b |
| 2 |
当x=0时,y=b,即OF=-b
∴tan∠OCB=
| OF |
| OC |
∴sin∠OCB=
| 2 | ||
|
2
| ||
| 5 |
(3)过A作AD⊥x轴,过B作BE⊥x轴
则AC=
| ||
| 2 |
| ||
| 2 |
BC=
| ||
| 2 |
| ||
| 2 |
∴AC-BC=
| ||
| 2 |
| 5 |
| 5 |
又-2x+b=
| k |
| x |
所以-2x2+bx-k=0
∴xA+xB=
| b |
| 2 |
∴-
| 5 |
| b |
| 2 |
| 5 |
∴b=-2
| 5 |
∴y=-2x-2
| 5 |
点评:这道题主要考查反比例函数的图象与一次函数的交点问题,借助图象分析之间的关系,体现数形结合思想的重要性.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
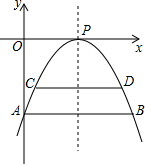 有一座抛物线形状的拱桥,当水位涨到AB时,水面AB的宽度为14米,如果水位再上升4米,就到达警戒水位CD,这时水面的宽度是10米.
有一座抛物线形状的拱桥,当水位涨到AB时,水面AB的宽度为14米,如果水位再上升4米,就到达警戒水位CD,这时水面的宽度是10米. (1)已知线段AB在平面内,在平面内找一点P使∠APB=90°.
(1)已知线段AB在平面内,在平面内找一点P使∠APB=90°.
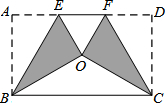 将矩形纸片ABCD按如图方式折叠,折痕是BE、CF,折叠后点A和点D重合在点O处,形成的△EOF是等边三角形,当
将矩形纸片ABCD按如图方式折叠,折痕是BE、CF,折叠后点A和点D重合在点O处,形成的△EOF是等边三角形,当 如图,AB、CD、EF相交于点O,∠1=20°,∠BOC=80°,则∠2=
如图,AB、CD、EF相交于点O,∠1=20°,∠BOC=80°,则∠2=