题目内容
19.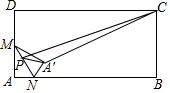 如图,在矩形ABCD中,AB=4,AD=2,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C.在MN上存在一动点P.连接A'P、CP,则△A'PC周长的最小值是$\sqrt{17}$-1+2$\sqrt{5}$.
如图,在矩形ABCD中,AB=4,AD=2,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C.在MN上存在一动点P.连接A'P、CP,则△A'PC周长的最小值是$\sqrt{17}$-1+2$\sqrt{5}$.
分析 分两步讨论:①先确定点P的位置,当A、P、C三点共线时,AP+PC有最小值,
②当M、A′、C三点共线时,A′C有最小值,确定动点N的位置;
再计算此时的周长即可.
解答 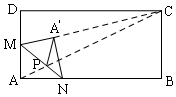 解:分两步:
解:分两步:
①连接AP,则AP=AP′,
∴△A'PC周长=A′P+PC+A′C=AP+PC+A′C,
∵AP+PC>AC,
当A、P、C三点共线时,AP+PC有最小值,是AC的长,
所以AC与MN的交点就是点P,
由勾股定理得:AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
②连接CM,
∵A′C>CM-A′M,
∴当M、A′、C三点共线时,A′C有最小值,
此时,∵M是AD的中点,
∴AM=DM=1,
∴MC=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,
由折叠得:AM=A′M=1,
∴A′C=MC-A′M=$\sqrt{17}$-1,
∴△A'PC周长的最小值是:$\sqrt{17}$-1+2$\sqrt{5}$,
故答案为:$\sqrt{17}$-1+2$\sqrt{5}$.
点评 本题考查了轴对称-最短路径问题和矩形的性质,有难度,还考查了两点之间线段最短,或利用三角形的三边关系来确定动点的位置.

练习册系列答案
相关题目
10.下列各式中,应用乘法公式计算正确的是( )
| A. | (x-y)(-y-x)=y2-x2 | B. | (2x-y)(y-2x)=-y2-4x2 | ||
| C. | (2a-1)2=4a2-2a+1 | D. | (3-x)2=9-x2 |
7.反比例函数y=$\frac{k}{x}$,若k<0,则( )
| A. | y的值为负 | |
| B. | 双曲线在一、三象限 | |
| C. | y随x的增大而增大 | |
| D. | 在所在的每一个象限,y随x的增大而增大 |
14.计算:(2ab2)3-(9ab2)(-ab2)2,结果正确的是( )
| A. | 17a3b6 | B. | 8a6b12 | C. | -a3b6 | D. | 15a3b6 |
4.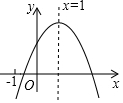 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
8. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 四棱锥 | C. | 圆柱 | D. | 四棱柱 |
9.若x2+a-x是关于x的完全平方式,则a的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | -$\frac{1}{4}$ |
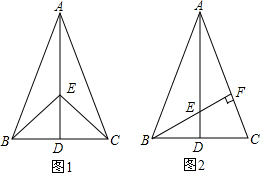
 二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+c>b;②4ac<b2;③2a+b>0.其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①a+c>b;②4ac<b2;③2a+b>0.其中正确的有( )