题目内容
2.在△ABC中,已知AC⊥BC,AC=12cm,BC=5cm,∠ACB的平分线交AB于点T,则BT的长为$\frac{65}{17}$.分析 如图,作TE⊥BC于E,TF⊥AC于F.由CT平分∠ACB,推出TE=TF,由$\frac{{S}_{△BCT}}{{S}_{△ACT}}$=$\frac{\frac{1}{2}•BC•ET}{\frac{1}{2}•AC•TF}$=$\frac{BT}{TA}$,推出$\frac{BT}{TA}$=$\frac{5}{12}$,∵AB=$\sqrt{{5}^{2}+1{2}^{2}}$=13,推出BT=$\frac{5}{17}$•AB,由此即可解决问题.
解答 解:如图,作TE⊥BC于E,TF⊥AC于F.
∵CT平分∠ACB,
∴TE=TF,
∵$\frac{{S}_{△BCT}}{{S}_{△ACT}}$=$\frac{\frac{1}{2}•BC•ET}{\frac{1}{2}•AC•TF}$=$\frac{BT}{TA}$,
∴$\frac{BT}{TA}$=$\frac{5}{12}$,∵AB=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴BT=$\frac{5}{17}$•AB=$\frac{65}{17}$,
故答案为$\frac{65}{17}$.
点评 本题考查勾股定理、角平分线的性质定理、三角形的面积等知识,解题的关键是学会添加常用辅助线,学会利用面积法证明线段之间的关系,属于中考常考题型.

练习册系列答案
相关题目
15.如果二次根式$\sqrt{x-2}$有意义,那么x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≠2 | D. | x≤2 |
12.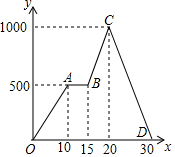 宇嘉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示.下列结论中,不正确的是( )
宇嘉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示.下列结论中,不正确的是( )
 宇嘉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示.下列结论中,不正确的是( )
宇嘉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示.下列结论中,不正确的是( )| A. | 整个行进过程花了30分钟 | B. | 整个行进过程共走了1000米 | ||
| C. | 在图中停下来休息了5分钟 | D. | 返回时速度为100米/分 |
19.如图是由棱长为1的正方体搭成的某几何体三视图,则图中棱长为1的正方体的个数是( )


| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
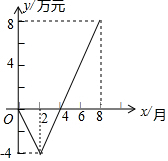 某超市今年年初因管理不善,效益较差,连续几个月出现亏损,后改革管理方法,实行股份制,员工积极性大增,业绩逐步上升,1-8月的累计利润y(万元)与时间x(月)之间的关系如图,根据图象回答:
某超市今年年初因管理不善,效益较差,连续几个月出现亏损,后改革管理方法,实行股份制,员工积极性大增,业绩逐步上升,1-8月的累计利润y(万元)与时间x(月)之间的关系如图,根据图象回答: