题目内容
3.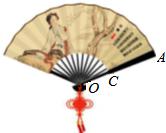 如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,则扇面的面积为$\frac{7nπ{a}^{2}}{120}$ (用代数式表示).
如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,则扇面的面积为$\frac{7nπ{a}^{2}}{120}$ (用代数式表示).
分析 根据题意求出OC的长,根据扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$计算即可.
解答 解:∵OA=5a,CA=3a,
∴OC=2a,
扇面的面积=$\frac{nπ×25{a}^{2}}{360}$-$\frac{nπ×4{a}^{2}}{360}$=$\frac{7nπ{a}^{2}}{120}$,
故答案为:$\frac{7nπ{a}^{2}}{120}$.
点评 本题考查的是扇形面积的计算,掌握扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列数据中不能作为直角三角形的三边长是( )
| A. | 1、1、$\sqrt{2}$ | B. | 5、12、13 | C. | 3、5、7 | D. | 6、8、10 |
18. 如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠AOC=80°,则∠D的度数为( )
如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠AOC=80°,则∠D的度数为( )
 如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠AOC=80°,则∠D的度数为( )
如图,AB为⊙O的直径,C,D为⊙O上的两点,若∠AOC=80°,则∠D的度数为( )| A. | 80° | B. | 60° | C. | 50° | D. | 40° |
13.二次函数y=(x-1)2+2的最小值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
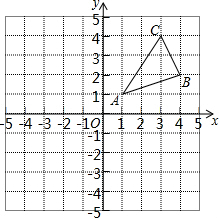 如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).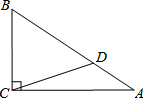 如图,Rt△ABC中,∠ACB=90°,cosA=$\frac{5}{6}$,D为AB上一点,且AD:BD=1:2,若BC=3$\sqrt{11}$,求CD的长.
如图,Rt△ABC中,∠ACB=90°,cosA=$\frac{5}{6}$,D为AB上一点,且AD:BD=1:2,若BC=3$\sqrt{11}$,求CD的长.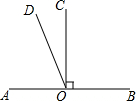 如图,已知直线AB,线段CO⊥AB于O,∠AOD=$\frac{1}{2}$∠BOD,求∠COD的度数.
如图,已知直线AB,线段CO⊥AB于O,∠AOD=$\frac{1}{2}$∠BOD,求∠COD的度数.