题目内容
8.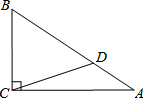 如图,Rt△ABC中,∠ACB=90°,cosA=$\frac{5}{6}$,D为AB上一点,且AD:BD=1:2,若BC=3$\sqrt{11}$,求CD的长.
如图,Rt△ABC中,∠ACB=90°,cosA=$\frac{5}{6}$,D为AB上一点,且AD:BD=1:2,若BC=3$\sqrt{11}$,求CD的长.
分析 过D作DE⊥AC于E,则DE∥BC.先在Rt△ABC中,由cosA=$\frac{AC}{AB}$=$\frac{5}{6}$,可设AC=5k,则AB=6k,利用勾股定理得出AB2-AC2=BC2,求出k=±3(负值舍去),那么AC=15,AB=18.再由DE∥BC,得出$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{1}{3}$,求出DE=$\frac{1}{3}$BC=$\sqrt{11}$,AE=$\frac{1}{3}$AC=5,CE=AC-AE=10,然后利用勾股定理得出CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{111}$.
解答 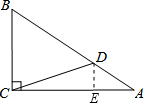 解:过D作DE⊥AC于E,则DE∥BC.
解:过D作DE⊥AC于E,则DE∥BC.
∵Rt△ABC中,∠ACB=90°,
∴cosA=$\frac{AC}{AB}$=$\frac{5}{6}$,
∴设AC=5k,则AB=6k,
∵AB2-AC2=BC2,
∴36k2-25k2=99,
∴k=±3(负值舍去),
∴AC=15,AB=18.
∵DE∥BC,
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{1}{3}$,
∴DE=$\frac{1}{3}$BC=$\sqrt{11}$,AE=$\frac{1}{3}$AC=5,
∴CE=AC-AE=10,
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{111}$.
点评 本题考查了解直角三角形,锐角三角函数的定义,平行线分线段成比例定理,勾股定理,难度适中.准确作出辅助线,构造CD为直角三角形的斜边是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若不等式0≤x+1<3的解中至少有一个能使关于x的一次不等式2x>a+3成立,则a的取值范围是( )
| A. | a≤1 | B. | a≥1 | C. | a≥-5 | D. | a<1 |
19.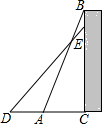 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )| A. | 0.4 | B. | 0.6 | C. | 0.7 | D. | 0.8 |
16. 某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )
某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )
 某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )
某校要举办国庆联欢会,主持人站在舞台的黄金分割点处最自然得体.如图,若舞台AB的长为20m,C为AB的一个黄金分割点(AC<BC),则AC的长为(结果精确到0.1m)( )| A. | 6.7m | B. | 7.6m | C. | 10m | D. | 12.4m |
20. 有理数a,b,c在数轴上的对应点的位置如图所示,这三个数中,绝对值最大的是( )
有理数a,b,c在数轴上的对应点的位置如图所示,这三个数中,绝对值最大的是( )
 有理数a,b,c在数轴上的对应点的位置如图所示,这三个数中,绝对值最大的是( )
有理数a,b,c在数轴上的对应点的位置如图所示,这三个数中,绝对值最大的是( )| A. | a | B. | b | C. | c | D. | 不能确定 |
17.已知一次函数y=(m-2)x+3的图象经过第一、二、四象限,则m的取值范围是( )
| A. | m<0 | B. | m>0 | C. | m<2 | D. | m>2 |
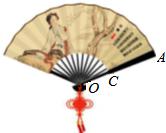 如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,则扇面的面积为$\frac{7nπ{a}^{2}}{120}$ (用代数式表示).
如图,折扇的骨柄OA的长为5a,扇面的宽CA的长为3a,折扇张开的角度为n°,则扇面的面积为$\frac{7nπ{a}^{2}}{120}$ (用代数式表示).