题目内容
19. 某校数学兴趣小组要测量天塔CD的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=27m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
某校数学兴趣小组要测量天塔CD的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=27m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
分析 首先根据题意得:∠CAD=45°,∠CBD=54°,AB=27m,在Rt△ACD中,易求得BD=AD-AB=CD-27;在Rt△BCD中,可得BD=CD•tan36°,即可得CD•tan36°=CD-27,继而求得答案.
解答 解:根据题意得:∠CAD=45°,∠CBD=54°,AB=27m,
∵在Rt△ACD中,∠ACD=∠CAD=45°,
∴AD=CD,
∵AD=AB+BD,
∴BD=AD-AB=CD-27(m),
∵在Rt△BCD中,tan∠BCD=$\frac{BD}{CD}$,∠BCD=90°-∠CBD=36°,
∴tan36°=$\frac{BD}{CD}$,
∴BD=CD•tan36°,
∴CD•tan36°=CD-27,
∴CD=$\frac{27}{1-tan36°}$≈$\frac{27}{1-0.73}$≈100(m).
答:天塔的高度CD约为:100m.
点评 本题考查了仰角的知识.此题难度适中,注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
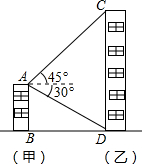 如图,甲楼AB的高度为21m,在甲楼楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°.求乙楼CD的高度(结果精确到0.1米,$\sqrt{3}$≈1.73,$\sqrt{2}$,1.41)
如图,甲楼AB的高度为21m,在甲楼楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°.求乙楼CD的高度(结果精确到0.1米,$\sqrt{3}$≈1.73,$\sqrt{2}$,1.41) 如图,直线AB、CD相交于点0,OE平分∠AOD,∠FOC=96°,∠BOF=40°,试求∠AOE的度数.
如图,直线AB、CD相交于点0,OE平分∠AOD,∠FOC=96°,∠BOF=40°,试求∠AOE的度数.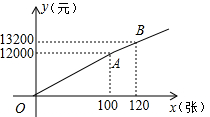 在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).
在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).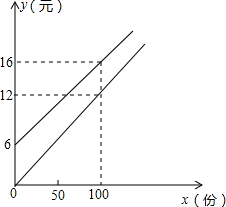 我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示: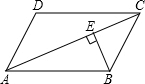 如图所示,在?ABCD中,AC=21cm,BE⊥AC于E,且BE=5cm,AD=7cm,则两条平行线AD与BC间的距离为15cm.
如图所示,在?ABCD中,AC=21cm,BE⊥AC于E,且BE=5cm,AD=7cm,则两条平行线AD与BC间的距离为15cm.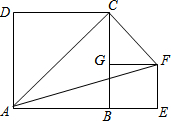 如图,正方形ABCD的边长为a,正方形BEFG的边长为b,
如图,正方形ABCD的边长为a,正方形BEFG的边长为b,