题目内容
给出下列四个命题:
(1)一组对边平行的四边形是平行四边形;
(2)一条对角线平分一个内角的平行四边形是菱形;
(3)两条对角线互相垂直的矩形是正方形;
(4)顺次连接对角线相等的四边形各边中点所得四边形是矩形.
其中正确命题的个数为 .
(1)一组对边平行的四边形是平行四边形;
(2)一条对角线平分一个内角的平行四边形是菱形;
(3)两条对角线互相垂直的矩形是正方形;
(4)顺次连接对角线相等的四边形各边中点所得四边形是矩形.
其中正确命题的个数为
考点:命题与定理
专题:
分析:根据平行四边形的判定对(1)进行判断;根据菱形的判定方法对(2)进行判断;根据正方形的判定方法对(3)进行判断;根据三角形中位线性质和矩形的判定方法对(4)进行判断.
解答:解:两组对边分别平行的四边形是平行四边形,所以(1)错误;
一条对角线平分一个内角的平行四边形是菱形,所以(2)正确;
两条对角线互相垂直的矩形是正方形,所(3)正确;
顺次连接对角线相等的四边形各边中点所得四边形是矩形,所以(4)正确.
故答案为:3.
一条对角线平分一个内角的平行四边形是菱形,所以(2)正确;
两条对角线互相垂直的矩形是正方形,所(3)正确;
顺次连接对角线相等的四边形各边中点所得四边形是矩形,所以(4)正确.
故答案为:3.
点评:本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
将4个红球、3个白球、2个黑球放入一个不透明的袋子里,从中摸出8个球,恰好红球、白球、黑球都摸到,这个事件是( )
| A、必然事件 | B、不可能事件 |
| C、随机事件 | D、不能确定 |
下列关于三角形全等的判定,其中正确的是( )
| A、有两边和第三边上的中线对应相等的两个三角形全等 |
| B、有两边和其中一边上的高对应相等的两个三角形全等 |
| C、有两边和第三边上的高对应相等的两个三角形全等 |
| D、三边中,有两边对应相等的两个三角形全等 |
若
=x,则x的取值范围是( )
| x2 |
| A、x≥0 | B、x≤0 |
| C、x>0 | D、x<0 |
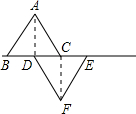 如图,已知△ABC和△DEF是两个边长为10cm的等边三角形,且B、D、C、E都在同一直线上.连接AD、CF.
如图,已知△ABC和△DEF是两个边长为10cm的等边三角形,且B、D、C、E都在同一直线上.连接AD、CF.