题目内容
13.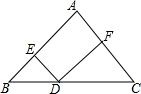 如图,在△ABC中,AB=AC=8,D是BC上一动点(D与B、C不重合),且DE∥AC,DF∥AB,则四边形DEAF的周长是16.
如图,在△ABC中,AB=AC=8,D是BC上一动点(D与B、C不重合),且DE∥AC,DF∥AB,则四边形DEAF的周长是16.
分析 根据等角对等边可得∠B=∠C,再根据两直线平行,同位角相等可得∠B=∠CDE,然后根据等角对等边可得CE=DE,同理可得BF=DF,然后求出四边形DEAF的周长=AB+AC,代入数据进行计算即可得解.
解答 解:∵AB=AC,
∴∠B=∠C,
∵DE∥AB,
∴∠B=∠CDE,
∴CE=DE,
同理可得BF=DF,
∴四边形DEAF的周长=AF+DF+DE+AE=AF+BF+CE+AE=AB+AC,
∵AB=AC=8,
∴四边形DEAF的周长=8+8=16.
故答案为:16.
点评 本题主要考查了等腰三角形的判定与性质,平行线的性质,熟记等腰三角形的性质与判定求出四边形DEAF的周长=AB+AC是解题的关键.

练习册系列答案
相关题目
2.要使分式$\frac{-5}{x-1}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x<1 | D. | x≠-1 |
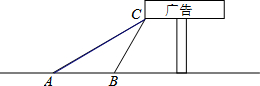 如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号)
如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号)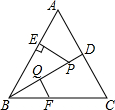 如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.如果BF=a,那么PE=$\frac{\sqrt{3}}{2}$a(用含a的代数式表示).
如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.如果BF=a,那么PE=$\frac{\sqrt{3}}{2}$a(用含a的代数式表示). 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.