��Ŀ����
��ͼ�������ź��������������������Σ���С����״����С����ͬ������ˮλʱ�����ˮ�����AB=20m������M��ˮ��6m����MO=6m����С����N��ˮ��4.5m����NC=4.5m������ˮλ���Ǹպ���ûС��ʱ������ͼ�е�ֱ������ϵ�����ʱ���ˮ�����EF��
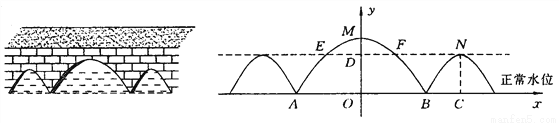
 ˮ�����Ϊ10m
���������������:���������ߵĽ���ʽΪһ��ʽ��ʽ,�ѵ�A(��10,0)�������ʽ���a=,��˺�������ʽΪ,����NC=4.5,��֪��E,F��������,�������ʽ���������E,F�ĺ�����,�̶��������EF.
�������:�������ߵĽ���ʽΪy=ax2+6,�������:B��10,0��,
��a��102+6=0,���a=��0.06,��y=��0.06x2+6,
��y=4....
ˮ�����Ϊ10m
���������������:���������ߵĽ���ʽΪһ��ʽ��ʽ,�ѵ�A(��10,0)�������ʽ���a=,��˺�������ʽΪ,����NC=4.5,��֪��E,F��������,�������ʽ���������E,F�ĺ�����,�̶��������EF.
�������:�������ߵĽ���ʽΪy=ax2+6,�������:B��10,0��,
��a��102+6=0,���a=��0.06,��y=��0.06x2+6,
��y=4....
 �Ķ��쳵ϵ�д�
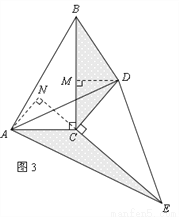
�Ķ��쳵ϵ�д���ͼ��ƽ���ı���ABCD���ܳ���26cm���Խ���AC��BD���ڵ�O��AC��AB��E��BC�е㣬��AOD���ܳ��ȡ�AOB���ܳ���3cm����AE�ij���Ϊ��������
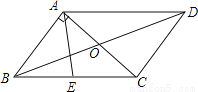
A. 3cm B. 4cm C. 5cm D. 8cm
 B
�������������������?ABCD���ܳ�Ϊ26cm��
��AB+AD=13cm��OB=OD��
�ߡ�AOD���ܳ��ȡ�AOB���ܳ���3cm��
�ࣨOA+OD+AD��-��OA+OB+AB��=AD-AB=3cm��
��AB=5cm��AD=8cm��
��BC=AD=8cm��
��AC��AB��E��BC�е㣬
��AE=BC=4cm.
��ѡB��
B
�������������������?ABCD���ܳ�Ϊ26cm��
��AB+AD=13cm��OB=OD��
�ߡ�AOD���ܳ��ȡ�AOB���ܳ���3cm��
�ࣨOA+OD+AD��-��OA+OB+AB��=AD-AB=3cm��
��AB=5cm��AD=8cm��
��BC=AD=8cm��
��AC��AB��E��BC�е㣬
��AE=BC=4cm.
��ѡB�� ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ������˵��������ǣ� ��
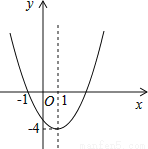
A��ͼ�����ֱ��x=1�Գ�
B������y=ax2+bx+c��a��0������Сֵ�ǩ�4
C����1��3�Ƿ���ax2+bx+c=0��a��0����������
D����x��1ʱ��y��x�����������
 D
��������
������������ݶԳ��ἰ��������x�ύ���������϶��κ��������ʣ����ɶ����ý��۽����жϣ�
��������
A���۲�ͼ��֪�����ߵĶԳ���Ϊֱ��x=1����ͼ�����ֱ��x=1�Գƣ���ȷ���ʱ�ѡ��������⣻
B���۲�ͼ��֪�����ߵĶ�������Ϊ��1����4�����������߿������ϣ����Ժ���y=ax2+bx+c��a��0������Сֵ�ǩ�4����ȷ���ʱ�ѡ��������⣻
C��...
D
��������
������������ݶԳ��ἰ��������x�ύ���������϶��κ��������ʣ����ɶ����ý��۽����жϣ�
��������
A���۲�ͼ��֪�����ߵĶԳ���Ϊֱ��x=1����ͼ�����ֱ��x=1�Գƣ���ȷ���ʱ�ѡ��������⣻
B���۲�ͼ��֪�����ߵĶ�������Ϊ��1����4�����������߿������ϣ����Ժ���y=ax2+bx+c��a��0������Сֵ�ǩ�4����ȷ���ʱ�ѡ��������⣻
C��... ����һö����Ӳ�ң���غ����泯�ϡ���һ�¼��ǣ�������
A. ��Ȼ�¼� B. ����¼� C. ȷ���¼� D. �������¼�
 B
����������������¼��Ķ��壬����¼����ǿ��ܷ�����Ҳ���ܲ��������¼��������жϣ�
��1ö����Ӳ�ң���غ�������泯�ϣ�Ҳ���ܷ��泯�ϣ�����1ö����Ӳ�ң���غ����泯��������¼�.
��ѡB.
B
����������������¼��Ķ��壬����¼����ǿ��ܷ�����Ҳ���ܲ��������¼��������жϣ�
��1ö����Ӳ�ң���غ�������泯�ϣ�Ҳ���ܷ��泯�ϣ�����1ö����Ӳ�ң���غ����泯��������¼�.
��ѡB. һ�������ĺ�����װ��2�������1���������dz���ɫ�ⶼ��ͬ����������������һ����������������ȷ����(����)
A. ���������DZ�Ȼ�¼�
B. ���������Dz������¼�
C. ������������������Ŀ��������
D. �����������������Ŀ����Դ�
 D
����������������¼��ĸ���Լ��������ľ͵õ����������ֱ�������ɣ�
��������
A����������������¼����ʴ�ѡ�����
B����������������¼����ʴ�ѡ�����
C�������������������Ŀ�������ȣ�
���ݲ����ĺ�����װ��2�������1�����ó������������������Ŀ����Դʴ�ѡ�����
D�����ݲ����ĺ�����װ��2�������1�����ó��������������...
D
����������������¼��ĸ���Լ��������ľ͵õ����������ֱ�������ɣ�
��������
A����������������¼����ʴ�ѡ�����
B����������������¼����ʴ�ѡ�����
C�������������������Ŀ�������ȣ�
���ݲ����ĺ�����װ��2�������1�����ó������������������Ŀ����Դʴ�ѡ�����
D�����ݲ����ĺ�����װ��2�������1�����ó��������������... ijһ�ͺŷɻ���½���еľ���y(��λ��m)�뻬��ʱ��x(��λ��s)֮��ĺ�����ϵʽ��y��60x��1.5x2�����ͺŷɻ���½���軬��________m����ͣ������
 600
�������������������y=60x��1.5x2=��1.5��x��20��2+600��
��x=20ʱ��yȡ�����ֵ����ʱy=600
600
�������������������y=60x��1.5x2=��1.5��x��20��2+600��
��x=20ʱ��yȡ�����ֵ����ʱy=600 ��ͼ1����������ȫ��ͬ��������ֽƬABC��DEC�غϷ��ã����С�C=90�㣬��B=��E=30��.
��1����������
��ͼ2���̶���ABC��ʹ��DEC�Ƶ�C��ת������Dǡ������AB����ʱ����գ�
���߶�DE��AC��λ�ù�ϵ��_________��
�����BDC�����ΪS1����AEC�����ΪS2����S1��S2��������ϵ��____________.
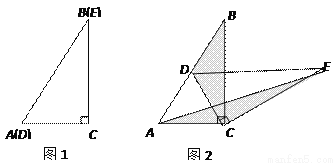
��2��������֤
����DEC�Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����S1��S2��������ϵ��Ȼ�����������Էֱ������ˡ�BDC�͡�AEC��BC��CE���ϵĸߣ�����֤��С���IJ���.
��3����չ̽��
��֪��ABC=60�㣬��D�����ƽ������һ�㣬BD=CD=4��DE//AB��BC�ڵ�E����ͼ4��.��������BA�ϴ��ڵ�F��ʹ ����ֱ��д����Ӧ��BF�ij�.
����ֱ��д����Ӧ��BF�ij�.

 ��1����DE��AC����S1��S2����2��֤������������3��BF�ij�Ϊ��.
�������������������1���ٸ�����ת�����ʿɵ�AC=CD��Ȼ�������ACD�ǵȱ������Σ����ݵȱ������ε����ʿɵá�ACD=60�㣬Ȼ������ڴ�����ȣ���ֱ��ƽ�н��
�ڸ��ݵȱ������ε����ʿɵ�AC=AD���ٸ���ֱ��������30������Ե�ֱ�DZߵ���б�ߵ�һ�����AC=AB��Ȼ�����AC=BD���ٸ��ݵȱ������ε�������...
��1����DE��AC����S1��S2����2��֤������������3��BF�ij�Ϊ��.
�������������������1���ٸ�����ת�����ʿɵ�AC=CD��Ȼ�������ACD�ǵȱ������Σ����ݵȱ������ε����ʿɵá�ACD=60�㣬Ȼ������ڴ�����ȣ���ֱ��ƽ�н��
�ڸ��ݵȱ������ε����ʿɵ�AC=AD���ٸ���ֱ��������30������Ե�ֱ�DZߵ���б�ߵ�һ�����AC=AB��Ȼ�����AC=BD���ٸ��ݵȱ������ε�������... һ��ͼ�����۾���ƽ�Ʊ任�����Ǿ�����ת�任������˵����ȷ���ǣ�������
�ٶ�Ӧ�߶�ƽ��
�ڶ�Ӧ�߶����
��ͼ�ε���״�ʹ�С��û�з����仯
�ܶ�Ӧ����ȣ�
A. �٢ڢ� B. �ڢۢ� C. �٢ڢ� D. �٢ۢ�
 B
����������������
��ƽ�ƺ��Ӧ�߶�ƽ�У���ת��Ӧ�߶β�һ��ƽ�У��ʱ�С�����
������ƽ�ƻ�����ת����Ӧ�߶���ȣ��ʱ�С����ȷ��
������ƽ�ƻ�����ת��ͼ�ε���״�ʹ�С��û�з����仯���ʱ�С����ȷ��
������ƽ�ƻ�����ת����Ӧ����ȣ��ʱ�С����ȷ��
����������˵����ȷ���Ǣڢۢܣ�
��ѡB��
B
����������������
��ƽ�ƺ��Ӧ�߶�ƽ�У���ת��Ӧ�߶β�һ��ƽ�У��ʱ�С�����
������ƽ�ƻ�����ת����Ӧ�߶���ȣ��ʱ�С����ȷ��
������ƽ�ƻ�����ת��ͼ�ε���״�ʹ�С��û�з����仯���ʱ�С����ȷ��
������ƽ�ƻ�����ת����Ӧ����ȣ��ʱ�С����ȷ��
����������˵����ȷ���Ǣڢۢܣ�
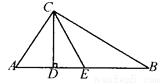
��ѡB�� ��֪����ͼ���ڡ�ABC�У���ACB��90�㣬CDΪ�ߣ�CEƽ�֡�BCD���ҡ�ACD����BCD��1��2����ôCE��AB���ϵ����߶���?˵�����ɣ�
 ������
������������������������ACD=30�㣬��BCD=60�㣬Ȼ����ݽ�ƽ���ߵĶ��������DCE=��BCE=30�㣬�ٸ���ֱ������������ǻ��������B����A���Ӷ��õ���A=��ACE����B=��BCE�����ݵȽǶԵȱߵ����ʿɵ�AE=EC��BE=EC��Ȼ�����AE=BE�����ɵý⣮
���������CE��AB���ϵ����ߡ�
���ɣ��ߡ�ACB=90�㣬��ACD:��BCD=1:2��
��...
������
������������������������ACD=30�㣬��BCD=60�㣬Ȼ����ݽ�ƽ���ߵĶ��������DCE=��BCE=30�㣬�ٸ���ֱ������������ǻ��������B����A���Ӷ��õ���A=��ACE����B=��BCE�����ݵȽǶԵȱߵ����ʿɵ�AE=EC��BE=EC��Ȼ�����AE=BE�����ɵý⣮
���������CE��AB���ϵ����ߡ�
���ɣ��ߡ�ACB=90�㣬��ACD:��BCD=1:2��
��... 
