题目内容
5.阅读理解在⊙I中,弦AF与DE相交于点Q,则AQ•QF=DQ•QE.你可以利用这一性质解决问题.
问题解决
如图,在平面直角坐标系中,等边△ABC的边BC在x轴上,高AO在y轴的正半轴上,点Q(0,1)是等边△ABC的重心,过点Q的直线分别交边AB、AC于点D、E,直线DE绕点Q转动,设∠OQD=α(60°<α<120°),△ADE的外接圆⊙I交y轴正半轴于点F,连接EF.
(1)填空:AB=2$\sqrt{3}$;
(2)在直线DE绕点Q转动的过程中,猜想:$\frac{AD}{DQ}$与$\frac{AE}{QE}$的值是否相等?试说明理由.
(3)①求证:AQ2=AD•AE-DQ•QE;
②记AD=a,AE=b,DQ=m,QE=m(a、b、m、n均为正数),请直接写出mn的取值范围.

分析 (1)如图1,连接BQ,由点Q(0,1)是等边△ABC的重心,得到AQ=BQ=2OQ=2,∠QBO=30°,根据等边三角形的性质即可得到结论;
(2)根据等边三角形的性质得到∠DAF=∠FAE,根据相似三角形的性质得到$\frac{AD}{DQ}$=$\frac{AF}{EF}$,根据相似三角形的性质得到$\frac{AF}{EF}$=$\frac{AE}{QE}$,等量代换即可得到结论;
(3)①由相似三角形的性质得到$\frac{AD}{AQ}=\frac{AF}{AE}$,根据线段的和差得到AD•AE=(AQ+QF)•AQ,化简即可得到结论;②如图2,过点E作ET⊥AB于T,解直角三角形得到E=AE•sin60°=$\frac{\sqrt{3}}{2}$b,求得S△ADE=$\frac{\sqrt{3}}{4}$ab,当α=90°时,此时DE∥x轴,S△ADE最小,根据相似三角形的性质得到$\frac{DE}{BC}=\frac{AQ}{AO}=\frac{2}{3}$,得到$\frac{{{S_{△ADE}}}}{{3\sqrt{3}}}=\frac{4}{9}$${S_{△ADE}}=\frac{4}{9}×3\sqrt{3}=\frac{{4\sqrt{3}}}{3}$,当α=120°时,此时DE经过点C,即点E和点C重合,S△ADE最大,根据三角形的面积得到$\frac{16}{3}≤ab≤6$,代入化简即可得到结论.
解答  解:(1)如图1,连接BQ,
解:(1)如图1,连接BQ,
∵点Q(0,1)是等边△ABC的重心,
∴AQ=BQ=2OQ=2,∠QBO=30°,
∴AO=3,
∴AB=sin60°•AO=2$\sqrt{3}$;
故答案为:2$\sqrt{3}$;
(2)相等,
理由:∵AO为等边△ABC的高,∴AO平分∠BAC,
∴∠DAF=∠FAE,又∠ADE=∠AFE,
∴△ADQ∽△AFE,
∴$\frac{AD}{DQ}$=$\frac{AF}{EF}$,
∵∠QEF=∠OAE,∠AFE=∠QFE,
∴△AFE∽△QEF,
∴$\frac{AF}{EF}$=$\frac{AE}{QE}$,
∴$\frac{AD}{DQ}$=$\frac{AE}{QE}$;
(3)①∵△ADQ∽△AFE,
∴$\frac{AD}{AQ}=\frac{AF}{AE}$,∴AD•AE=AF•AQ,即AD•AE=(AQ+QF)•AQ,
∴AD•AE=AQ2+AQ•QF,∵AQ•QF=DQ•QE,
∴AD•AE=AQ2+DQ•QE,
即AQ2=AD•AE-DQ•QE;
②如图2,过点E作ET⊥AB于T,
在Rt△AET中,∠EAT=60°,ET=AE•sin60°=$\frac{\sqrt{3}}{2}$b,S△ADE=$\frac{1}{2}$AD•ET=$\frac{1}{2}$AD•$\frac{\sqrt{3}}{2}$AE=$\frac{\sqrt{3}}{4}$AD•AE=$\frac{\sqrt{3}}{4}$ab,
当α=90°时,此时DE∥x轴,S△ADE最小,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AQ}{AO}=\frac{2}{3}$,
∴$\frac{{{S_{△ADE}}}}{{{S_{△ABC}}}}={({\frac{DE}{BC}})^2}=\frac{4}{9}$,
又∵S△ABC=$\frac{\sqrt{3}}{4}$×(2$\sqrt{3}$)2=3$\sqrt{3}$,
∴$\frac{{{S_{△ADE}}}}{{3\sqrt{3}}}=\frac{4}{9}$${S_{△ADE}}=\frac{4}{9}×3\sqrt{3}=\frac{{4\sqrt{3}}}{3}$,
当α=120°时,此时DE经过点C,即点E和点C重合,S△ADE最大,
∴S△ADE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×3$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$,
∴$\frac{{4\sqrt{3}}}{3}≤{S_{△ADE}}≤\frac{{3\sqrt{3}}}{2}$,即$\frac{{4\sqrt{3}}}{3}≤\frac{{\sqrt{3}}}{4}ab≤\frac{{3\sqrt{3}}}{2}$,
∴$\frac{{4\sqrt{3}}}{3}≤\frac{{\sqrt{3}}}{4}ab≤\frac{{3\sqrt{3}}}{2}$,$\frac{16}{3}≤ab≤6$,
由①证得:AQ2=AD•AE-DQ•QE,即22=ab-mn,
∴ab=mn+4,
∴$\frac{16}{3}$≤mn+4<6,
即$\frac{4}{3}$≤mn<2.
点评 本题考查了等边三角形的性质,圆周角定理,相似三角形的判定和性质,三角形面积的计算,旋转的性质,正确的作出辅助线构造直角三角形是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | πcm2 | B. | $\sqrt{3}$πcm2 | C. | 2πcm2 | D. | 4πcm2 |
| A. | $1-\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $1-\sqrt{2}$或$1+\sqrt{2}$ | D. | $1+\sqrt{2}$或-1 |
| A. | a | B. | 2a | C. | 8a | D. | -8a |
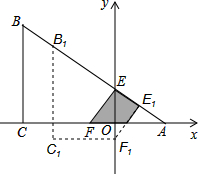 如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.
如图,有一张直角三角形纸片ABC,∠ACB=90°,∠B=60°,BC=3,直角边AC在x轴上,B点在第二象限,A($\sqrt{3}$,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在的直线上,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA方向平行移动,至B点到达A点停止(记平移后的四边形为B1C1F1E1).在平移过程中,设平移的距离BB1=x,四边形B1C1F1E1与△AEF重叠的面积为S.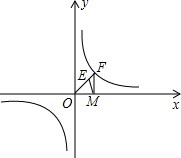 已知:反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(1,1)
已知:反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B(1,1) 在平面直角坐标系中,已知点A(-1,0),B(-2,2),请在图中画出线段AB,并画出线段AB绕点O逆时针旋转90°后的图形.
在平面直角坐标系中,已知点A(-1,0),B(-2,2),请在图中画出线段AB,并画出线段AB绕点O逆时针旋转90°后的图形.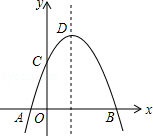 如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题: