题目内容
17.观察下列一组数:-$\frac{1}{4}$,$\frac{3}{9}$,-$\frac{5}{16}$,$\frac{7}{25}$,-$\frac{9}{36}$,…,它们是按一定规律排列的,那么这一组数的第n个数是(-1)n$\frac{2n-1}{(n+1)^{2}}$.分析 观察已知一组数发现:分子为从1开始的连续奇数,分母为从2开始的连续正整数的平方,单数项为负,双数项为正,写出第n个数即可.
解答 解:根据题意得:这一组数的第n个数是(-1)n$\frac{2n-1}{(n+1)^{2}}$.
故答案为:(-1)n$\frac{2n-1}{(n+1)^{2}}$.
点评 此题考查了规律型:数字的变化类,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
16. 由4个正方体搭成的几何体按如图放置,若要求画出它的三视图,则在所画的俯视图中正方形共有( )
由4个正方体搭成的几何体按如图放置,若要求画出它的三视图,则在所画的俯视图中正方形共有( )
 由4个正方体搭成的几何体按如图放置,若要求画出它的三视图,则在所画的俯视图中正方形共有( )
由4个正方体搭成的几何体按如图放置,若要求画出它的三视图,则在所画的俯视图中正方形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.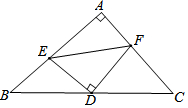 如图,在△ABC中,∠A=90°,点D是BC的中点,过点D作DE⊥DF分别AB、AC于点E、F.若BE=1.5,CF=2,则EF的长是( )
如图,在△ABC中,∠A=90°,点D是BC的中点,过点D作DE⊥DF分别AB、AC于点E、F.若BE=1.5,CF=2,则EF的长是( )
 如图,在△ABC中,∠A=90°,点D是BC的中点,过点D作DE⊥DF分别AB、AC于点E、F.若BE=1.5,CF=2,则EF的长是( )
如图,在△ABC中,∠A=90°,点D是BC的中点,过点D作DE⊥DF分别AB、AC于点E、F.若BE=1.5,CF=2,则EF的长是( )| A. | 2.4 | B. | 2.5 | C. | 3 | D. | 3.5 |
12.一个三角形的高的交点恰是三角形的顶点,则这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
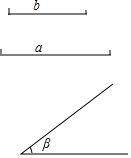 画△ABC,使其两边为已知线段a、b,夹角为β.(要求:用尺规作图,写出己知,求作;保留作图痕迹;不在已知的线、角上作图;不写作法).
画△ABC,使其两边为已知线段a、b,夹角为β.(要求:用尺规作图,写出己知,求作;保留作图痕迹;不在已知的线、角上作图;不写作法).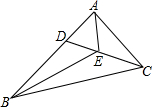 在△ABC中,点D为AB边上一点,BD=2AD,点E为CD的中点,若S△ADE=2,则S△ABC=12.
在△ABC中,点D为AB边上一点,BD=2AD,点E为CD的中点,若S△ADE=2,则S△ABC=12.