Question

3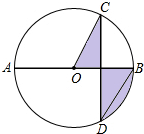．如图，AB是⊙O的直径，弦CD⊥AB，∠COB=60°，CD=2$\sqrt{3}$，则阴影部分图形的（　　）

• A． 4π
• B． 2π
• C． π
• D． $\frac{2π}{3}$

Answer 1

分析 如图，首先求出CE=$\sqrt{3}$；其次求出CO=2；运用S_阴影=S_扇形BOC，即可解决问题．

解答 解：如图，∵AB是⊙O的直径，弦CD⊥AB，
∴CE=DE=$\frac{1}{2}$CD=$\sqrt{3}$；
∵sin∠COB=$\frac{CE}{CO}$，且∠COB=60°，
∴CO=2；
由圆的对称性知：S_阴影=S_扇形BOC=$\frac{60π•{2}^{2}}{360}$=$\frac{2π}{3}$，
故选D．

点评 该题主要考查了扇形的面积公式、垂径定理等知识点及其应用问题；牢固掌握扇形的面积公式、垂径定理等知识点是解题的关键．