题目内容
12.已知抛物线y=x2-(m2+4)x-2m2-12(1)证明:无论m取何实数,抛物线与x轴恒有两个交点,且一个交点是(-2,0);
(2)m为何值时,两交点之间的距离为12;
(3)m为何值时,两交点间的距离最小.
分析 (1)令y=0,得到一个关于x的方程,利用判别式可判定结果;把(-2,0)代入可得出结论;
(2)令y=0,可求得方程的两个根,可表示出两交点的距离,令其为12可求得m;
(3)同(2)可表示出两交点间的距离,利用函数的增减性可求得m的值.
解答 (1)证明:在y=x2-(m2+4)x-2m2-12中,令y=0可得x2-(m2+4)x-2m2-12=0,
∵△=(m2+4)2+4(2m2+12)=m4+64>0,
∴方程x2-(m2+4)x-2m2-12=0有两个不相等的实数根,
∴无论m取何实数,抛物线与x轴恒有两个交点,
当x=-2时,代入可得y=4+2(m2+4)-2m2-12=0,
∴抛物线与x轴的一个交点坐标为(-2,0);
(2)解:令y=0可得x2-(m2+4)x-2m2-12=0,可解得x=-2或x=m2+6,
设与x轴的两个交点分别为A、B,
则AB=|m2+6-(-2)|=m2+8,
当AB=12时,则m2+8=12,解得m=±2,
即当m为±2时,抛物线与x轴的两交点间的距离为12;
(3)解:由(2)可知两交点间的距离为AB=m2+8,
为开口向上,对称轴为y轴的抛物线,
∴当m=0时,AB有最小值,
即当m=0时,抛物线与x轴两交点间的距离最小.
点评 本题主要考查二次函数与方程的关系,掌握二次函数与x轴的交点横坐标是对应一元二次方程的根是解题的关键,注意函数增减性的应用.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
2.用配方法解关于x的一元二次方程x2-2x-5=0,配方正确的是( )
| A. | (x+1)2=6 | B. | (x-1)2=6 | C. | (x-1)2=4 | D. | (x+1)2=4 |
3.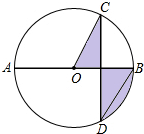 如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )
如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )
如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{2π}{3}$ |
7.对方程组$\left\{\begin{array}{l}{x+2y=-5}\\{4x-2y=13}\end{array}\right.$使用代入消元法变形正确的是( )
| A. | x=5-2y | B. | x=-5-2y | C. | y=$\frac{13+7x}{2}$ | D. | x=$\frac{13-2y}{7}$ |
4.$\frac{\sqrt{2}}{2}$是一个( )
| A. | 整数 | B. | 分数 | C. | 有理数 | D. | 无理数 |
1.下列运算正确的是( )
| A. | $\sqrt{4}$=2 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | 2-3=8 | D. | 20=0 |
 如图,OC⊥OD,∠2=54°08′,则∠1=35°52′.
如图,OC⊥OD,∠2=54°08′,则∠1=35°52′.