题目内容
11. 对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把
对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1)令P0(2,-3),O为坐标原点,则d(O,P0)=5;
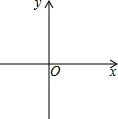
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离. 若P(a,-3)到直线y=x+1的直角距离为6,求a的值.
分析 (1)由P0与原点O的坐标,利用题中的新定义计算即可得到结果;
(2)利用题中的新定义列出x与y的关系式,画出相应的图象即可;
(3)设直线y=x+1上一点Q(x,x+1),表示出d(P,Q),由P(a,-3)到直线y=x+1的直角距离为6列出方程,分类讨论a与x的正负,利用绝对值的代数意义化简,求出a的值即可.
解答  解:(1)根据题意得:d(O,P0)=|2-0|+|-3-0|=2+3=5;
解:(1)根据题意得:d(O,P0)=|2-0|+|-3-0|=2+3=5;
故答案为:5;
(2)由题意,得|x|+|y|=1,
所有符合条件的点P组成的图形如图所示;
(3)∵P(a,-3)到直线y=x+1的“直角”距离为6,
∴设直线y=x+1上一点Q(x,x+1),则d(P,Q)=6,
∴|a-x|+|-3-x-1|=6,即|a-x|+|x+4|=6,
当a-x≥0,x≥-4时,原式=a-x+x+4=6,解得a=2;
当a-x<0,x<-4时,原式=x-a-x-4=6,解得a=-10,
综上,a的值为2或-10.
点评 此题属于一次函数综合题,涉及的知识有:绝对值的代数意义,利用了分类讨论的思想,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
1.下列命题是真命题的个数有( )
①直角三角形的两锐角互余;
②如果两个三角形的对应角相等,那么这两个三角形全等;
③在直角三角形中,若两条直角边长为n2-1和2n,则斜边长为n2+1;
④等腰三角形面积为12,底边上的高为4,则腰长为5.
①直角三角形的两锐角互余;
②如果两个三角形的对应角相等,那么这两个三角形全等;
③在直角三角形中,若两条直角边长为n2-1和2n,则斜边长为n2+1;
④等腰三角形面积为12,底边上的高为4,则腰长为5.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.用配方法解关于x的一元二次方程x2-2x-5=0,配方正确的是( )
| A. | (x+1)2=6 | B. | (x-1)2=6 | C. | (x-1)2=4 | D. | (x+1)2=4 |
6.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{27}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{{a}^{2}+{a}^{3}}$ | D. | $\sqrt{{a}^{2}-{b}^{2}}$ |
3.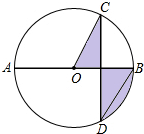 如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )
如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )
如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{2π}{3}$ |
1.下列运算正确的是( )
| A. | $\sqrt{4}$=2 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | 2-3=8 | D. | 20=0 |
 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为3.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为3.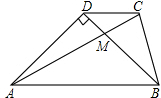 如图所示,在梯形ABCD中,AB∥CD,两对角线交于M,若AD=BD,AC=AB,∠ADB=90°,试说明:
如图所示,在梯形ABCD中,AB∥CD,两对角线交于M,若AD=BD,AC=AB,∠ADB=90°,试说明: 如图,OC⊥OD,∠2=54°08′,则∠1=35°52′.
如图,OC⊥OD,∠2=54°08′,则∠1=35°52′.