题目内容
14. 已知:如图,在△ABC中,AD是BC边上的高,CE是中线,F是CE的中点,CD=$\frac{1}{2}$AB,求证:DF⊥CE.
已知:如图,在△ABC中,AD是BC边上的高,CE是中线,F是CE的中点,CD=$\frac{1}{2}$AB,求证:DF⊥CE.
分析 连接DE,根据直角三角形斜边上的中线等于斜边的一半可得DE=$\frac{1}{2}$AB,再求出DE=CD,然后根据等腰三角形三线合一的性质证明即可.
解答  证明:连接DE,
证明:连接DE,
∵AD是BC边上的高,在Rt△ADB中,CE是中线,
∴DE=$\frac{1}{2}$AB,
∵CD=$\frac{1}{2}$AB,
∴DC=DE,
∵F是CE中点,
∴DF⊥CE.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并作辅助线构造出等腰三角形是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
2.用配方法解关于x的一元二次方程x2-2x-5=0,配方正确的是( )
| A. | (x+1)2=6 | B. | (x-1)2=6 | C. | (x-1)2=4 | D. | (x+1)2=4 |
6.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{27}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{{a}^{2}+{a}^{3}}$ | D. | $\sqrt{{a}^{2}-{b}^{2}}$ |
3.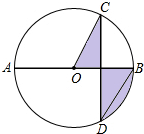 如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )
如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )
如图,AB是⊙O的直径,弦CD⊥AB,∠COB=60°,CD=2$\sqrt{3}$,则阴影部分图形的( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{2π}{3}$ |
4.$\frac{\sqrt{2}}{2}$是一个( )
| A. | 整数 | B. | 分数 | C. | 有理数 | D. | 无理数 |
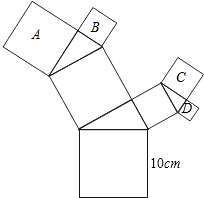 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为5cm、B的边长为6cm、C的边长为5cm,则正方形D的边长为$\sqrt{14}$cm.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为5cm、B的边长为6cm、C的边长为5cm,则正方形D的边长为$\sqrt{14}$cm. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为3.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为3.