题目内容
 彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )
彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )| A、(2n-1,2n) | ||
B、(2n-
| ||
C、(2n-1-
| ||
| D、(2n-1-1,2n-1) |
考点:相似多边形的性质,一次函数图象上点的坐标特征
专题:规律型
分析:根据矩形的性质求出点A1、A2的坐标,然后利用待定系数法求一次函数解析式求出k、b,从而得到一次函数解析式,再根据一次函数图象上点的坐标特征求出A3的坐标,然后求出B3的坐标,…,最后根据点的坐标特征的变化规律写出Bn的坐标即可.
解答:解:∵B1(1,2),
∴相似矩形的长是宽的2倍,
∵点B1、B2的坐标分别为(1,2),(3,4),
∴A1(0,2),A2(1,4),
∵点A1,A2在直线y=kx+b上,
∴
,
解得
,
∴y=2x+2,
∵点A3在直线y=2x+2上,
∴y=2×3+2=8,
∴点A3的坐标为(3,8),
∴点B3的横坐标为3+
×8=7,
∴点B3(7,8),
…,
Bn的坐标为(2n-1,2n).
故选A.
∴相似矩形的长是宽的2倍,
∵点B1、B2的坐标分别为(1,2),(3,4),
∴A1(0,2),A2(1,4),
∵点A1,A2在直线y=kx+b上,
∴
|
解得
|
∴y=2x+2,
∵点A3在直线y=2x+2上,
∴y=2×3+2=8,
∴点A3的坐标为(3,8),
∴点B3的横坐标为3+
| 1 |
| 2 |
∴点B3(7,8),
…,
Bn的坐标为(2n-1,2n).
故选A.
点评:本题考查了相似多边形的性质,一次函数图象上点的坐标特征,根据点A的系列坐标判断出相应矩形的长,再求出宽,然后得到点B的系列坐标的变化规律是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知4x-5y=0,则
=( )
| x |
| y |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
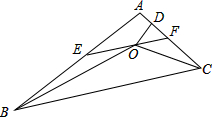 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;
②∠BOC=90°+
| 1 |
| 2 |
③EF不能成为△ABC的中位线;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
| A、①②③ | B、①②④ |
| C、②③④ | D、①③④ |
下列判断中,你认为正确的是( )
| A、0的倒数是0 | ||
B、
| ||
C、
| ||
D、
|
已知m<2,点A(x1,y1)、B(x2,y2)在双曲线y=
上,如果x1<x2,那么y1与y2的大小关系是( )
| 2-m |
| x |
| A、y1=y2 |
| B、y1>y2 |
| C、y1<y2 |
| D、无法确定 |
下列四个实数中,最小的数是( )
| A、0.01 | ||
B、-
| ||
| C、-0.1 | ||
| D、-2 |

 如图,菱形ABCD的对角线交于O点,DE∥AC,CE∥BD,
如图,菱形ABCD的对角线交于O点,DE∥AC,CE∥BD,