题目内容
已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.设y=x1+x2,则y最小值为 .
考点:一次函数的性质,根的判别式,根与系数的关系
专题:计算题
分析:先把方程化为一般式得到x2+2(m-1)x+m2=0,再根据判别式的意义得到m的取值范围为m≤
,然后根据根与系数的关系得到y=x1+x2=-2m+2,再根据一次函数的性质得当m=
时,y最小,则把m=
代入y=-2m+2中计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:方程整理为x2+2(m-1)x+m2=0,
根据题意得△=4(m-1)2-4m2≥0,解得m≤
,
y=x1+x2=-2(m-1)
=-2m+2,
∵y随m的增大而减小,
∴当m=
时,y最小,y的最小值=-2×
+2=1.
故答案为1.
根据题意得△=4(m-1)2-4m2≥0,解得m≤
| 1 |
| 2 |
y=x1+x2=-2(m-1)
=-2m+2,
∵y随m的增大而减小,
∴当m=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为1.
点评:本题考查了一次函数的性质:一次函数y=kx+b(k≠0),当k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.由于y=kx+b与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.也考查了根的判别式和根与系数的关系.

练习册系列答案
相关题目
下列判断中,你认为正确的是( )
| A、0的倒数是0 | ||
B、
| ||
C、
| ||
D、
|
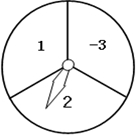 如图转盘,分成三个相同的扇形,3个扇形分别标有数字1、2、-3,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,重新转动转盘).
如图转盘,分成三个相同的扇形,3个扇形分别标有数字1、2、-3,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,重新转动转盘).
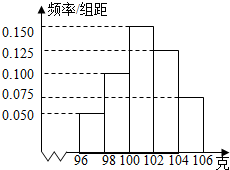 某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的 产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是
某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的 产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是