题目内容
11.(1)$\left\{\begin{array}{l}2x+3y=28\\ 6x-y=4\end{array}\right.$(2)解不等式组:$\left\{\begin{array}{l}5x+12>6-3x\\ \frac{4+x}{3}-1≥\frac{1-x}{3}\end{array}\right.$.
分析 (1)先用加减消元法求出x的值,再用代入消元法求出y的值即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)$\left\{\begin{array}{l}2x+3y=28①\\ 6x-y=4②\end{array}\right.$,①+②×3得,2x+3y+18x-3y=28+12,解得x=2,把x=2代入②得,12-y=4,解得y=8,
故方程组的解为$\left\{\begin{array}{l}x=2\\ y=8\end{array}\right.$;
(2)$\left\{\begin{array}{l}5x+12>6-3x①\\ \frac{4+x}{3}-1≥\frac{1-x}{3}②\end{array}\right.$,由①得,x>-$\frac{3}{4}$,由②得,x≥0,
故不等式组的解集为x≥0.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的法则是解答此题的关键.

练习册系列答案
相关题目
1.在数轴上,点A表示-3,从点A出发,沿数轴移动5个单位长度到达点B,则点B所表示的数为( )
| A. | 2 | B. | -8 | C. | 2或-8 | D. | 以上均不对 |
6.已知点P(3-a,a+1)在第四象限,则a的取值范围是( )
| A. | a>3 | B. | -1<a<2 | C. | a<-1 | D. | a<1 |
16.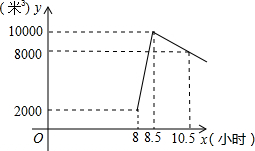 星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
(1)8:00~8:30,燃气公司向储气罐注入了8000米3的天然气;
(2)当x≥8.5时,求储气罐中的储气量y(米3)与时间x(小时)的函数关系式y=-1000x+18500;
(3)正在排队等候的20辆车加完气后,储气罐内还有天然气9600米3;
(4)这第20辆车在当天9:00之前不能加完气;
其中说法正确的有( )
 星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
星期天8:00∽8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.(1)8:00~8:30,燃气公司向储气罐注入了8000米3的天然气;
(2)当x≥8.5时,求储气罐中的储气量y(米3)与时间x(小时)的函数关系式y=-1000x+18500;
(3)正在排队等候的20辆车加完气后,储气罐内还有天然气9600米3;
(4)这第20辆车在当天9:00之前不能加完气;
其中说法正确的有( )
| A. | (1)(2) | B. | (2)(3) | C. | (1)(2)(3) | D. | (1)(2)(3)(4) |
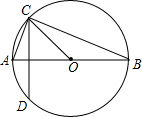 如图,AB是⊙O的直径,弦CD垂直AB,已知AC=1,BC=2$\sqrt{2}$,那么sin∠ACD的值是$\frac{1}{3}$.
如图,AB是⊙O的直径,弦CD垂直AB,已知AC=1,BC=2$\sqrt{2}$,那么sin∠ACD的值是$\frac{1}{3}$.