题目内容
7. 观察右边文本框中的各式:
观察右边文本框中的各式:猜想13+23+33+…+103=552.
分析 由题意可知:从1开始的连续自然数的立方和等于这些数的和的平方,由此得出答案即可.
解答 解:∵13=12,
13+23=(1+2)2,
13+23+33=(1+2+3)2,
13+23+33+43=(1+2+3+4)2
…
∴13+23+33+…+103=(1+2+3+4+…+10)2=552.
故答案为:552.
点评 本题考查数字变化规律,观察出从1开始的连续自然数的立方和等于这些数的和的平方是解题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
12.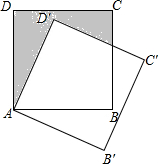 如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )
如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )
 如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )
如图,边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置,则图中阴影部分的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1-$\frac{\sqrt{3}}{3}$ | D. | 1-$\frac{\sqrt{3}}{4}$ |
17.下列实数中是无理数的是( )
| A. | -$\sqrt{4}$ | B. | $\root{3}{8}$ | C. | π0 | D. | -$\frac{\sqrt{2}}{2}$ |
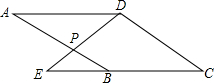 如图,?ABCD中,点P是AB边上的一动点(但不与A,B两点重合),DP的延长线交CB的延长线于点E.
如图,?ABCD中,点P是AB边上的一动点(但不与A,B两点重合),DP的延长线交CB的延长线于点E.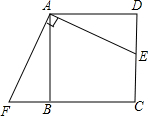 如图,已知E是正方形ABCD中CD上一点,延长BC到点F,使得BF=DE.
如图,已知E是正方形ABCD中CD上一点,延长BC到点F,使得BF=DE.