题目内容
19.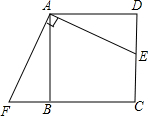 如图,已知E是正方形ABCD中CD上一点,延长BC到点F,使得BF=DE.
如图,已知E是正方形ABCD中CD上一点,延长BC到点F,使得BF=DE.(1)求证:△ABF≌△ADE;
(2)将△ADE以点A为中心,顺时针旋转90度得到△ABF.
分析 (1)根据SAS定理,即可证明两三角形相似;
(2)将△ADE顺时针旋转后与△ABF重合,A不变,因而旋转中心是A,∠DAB是旋转角,是90度.
解答 解:(1)∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°,
∴∠ABF=∠D=90°,
在△ABF与△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABF=∠D}\\{BF=DE}\end{array}\right.$,
∴△ABF≌△ADE;
(2)将△ADE以点A为中心,顺时针旋转90度得到△ABF.
故答案为:A.90°.
点评 本题主要考查了三角形全等的判定方法,以及旋转的定义,正确理解旋转的定义是解决本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
18. 如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
 如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
如图,在△ABC中,∠A=50°,∠C=70°,则外角∠ABD的度数是( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
19.关于x的不等式组$\left\{\begin{array}{l}x>a\\ x>1\end{array}\right.$的解集为x>1,则a的取值范围是( )
| A. | a>1 | B. | a<1 | C. | a≥1 | D. | a≤1 |
4. 某单位3月上旬中的1至6日每天用水量的变化如图所示,那么这6天用水量的中位数是( )
某单位3月上旬中的1至6日每天用水量的变化如图所示,那么这6天用水量的中位数是( )
 某单位3月上旬中的1至6日每天用水量的变化如图所示,那么这6天用水量的中位数是( )
某单位3月上旬中的1至6日每天用水量的变化如图所示,那么这6天用水量的中位数是( )| A. | 31.5 | B. | 32 | C. | 32.5 | D. | 33 |
 观察右边文本框中的各式:
观察右边文本框中的各式: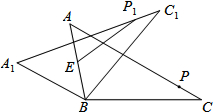 如图,在△ABC中,AB=6,BC=8,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,则线段EP1长度的最小值为1.
如图,在△ABC中,AB=6,BC=8,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,则线段EP1长度的最小值为1.